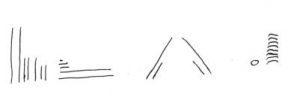Version vom 27.10.2006 (22.09.06)

Mathematik lernen

Spieltheorie ist Mathematik. Deshalb kommen viele Besucher (oft LehrerInnen und SchülerInnen) auf meine Seite, um hier die unmathematische Seite der Mathematik zu erleben. Lassen Sie mich deshalb einmal der Frage nachgehen, wieso viele Menschen Mathematik „einfach nicht verstehen“ und was man dagegen tun kann. 
Strukturen sind die Waffen der Mathematiker.
(Nicolas Bourbaki, Autorenkollektiv)

Ein Inhalt wird dazu in algebraische Formeln eingeschlossen,
damit man, indem man die Formel anwendet,
nicht hundertmal ein und dasselbe
wiederholen muss. (A. I. Herzen – wer immer das ist)

Meine Vermutung ist, dass das Schicksal schon in der Grundschule seinen Lauf nimmt. Und zwar, weil dort unter dem Etikett der Mathematik antimathematisches Denken gelehrt wird. Verstehen Sie mich nicht falsch: Ich habe nichts gegen unmathematisches Denken. Genausowenig wie gegen mathematisches Denken. Aber ich habe etwas dagegen, dass sich die eine Form des Denkens dort einschleicht, wo die andere gelehrt werden soll. Und bitte verstehen Sie mich auch ein zweites Mal nicht falsch: Ich spreche hier nicht über schlechte LehrerInnen, sondern über ein kulturell falsches Verständnis von Mathematik, das sich schon in der Konstruktion der Lehrpläne und Schulbücher äußert.

Lassen Sie mich ein Beispiel geben. In einem Mathematikbuch der zweiten Grundschulklasse (ich würde es nicht Mathe-, sondern Rechenbuch nennen, aber lassen wir das hier beiseite) findet sich folgender Aufgabentyp:

Ergänze bis zum nächsten Zehner:

5 + ? = 10
7 + ? = 10
usw.

Es ist klar, wozu man diese Aufgabe macht: Sie ist eine wichtige Voraussetzung fürs Kopfrechnen und fürs schriftliche Rechnen. Um schnell ohne Taschenrechner rechnen zu können, muss man auf Anhieb auswendig wissen, wie weit eine Zahl vom „Zehnerübergang“ entfernt ist.

Blättern wir im Buch einige Seiten weiter. Die Rechenaufgaben werden schwieriger, und irgendwo finden wir Aufgaben vom Typ:

36 + ? = 47

Das scheint das gleiche zu sein wie oben, also völlig harmlos. Und dennoch liegt genau hier der Schlüssel für die Volkskrankheit der (vermeintlichen) Mathematik-Unfähigkeit, die in Deutschland geradezu endemisch verbreitet ist. (Etwa ein Drittel meiner StudentInnen, die mit exzellenten Abiturnoten an die Hochschulen kommen, haben eine ausgeprägte Mathematikunwissenheit und halten sich für mathematisch unbegabt.) Wieso ist 36 +  = 47 keine harmlose Aufgabe? Weil es unmöglich ist, sie so zu lösen, wie sie hier steht. Beim Zehnerübergang gibt es nur neun Fälle, die man alle auswendig lernen kann (und auch sollte). Bei zweistelligen Zahlen wäre es vollkommen unsinnig, alle Abstände auswendig zu lernen, daher braucht man eine methodische Vorgehensweise, das Ergebnis auszurechnen. Das methodische Vorgehen besteht in diesem Fall darin, dass man auf die Gleichung einen Umformungsschritt anwendet, das Fragezeichen (meist als Kästchen dargestellt) freistellt und dadurch eine einfache Anweisung gibt, wie man den Wert ausrechnet, der dem Fragezeichen zugeordnet werden soll.

Das geht so: Wir wissen, dass man auf beiden Seiten der Gleichung dieselbe Operation ausführen darf und dass dadurch die Gleichheit nicht zerstört wird (zumindest bei der Addition funktioniert das). Also ziehen wir auf beiden Seiten 36 ab und erhalten:

36 + ? – 36 = 47-36
36 – 36 +  ? = 47-36 (Kommutativgesetz)
0 + ? = 47-36
? = 11

Lächerlich, stimmt’s? Viel zu umständlich. Wir wissen doch, dass man einfach 36 von 47 abziehen muss, wenn man den Abstand zwischen den beiden Zahlen ausrechnen möchte. Deshalb lernen wir in der Grundschule, dass man hier die „Umkehraufgabe“ rechnen muss. Also dass wir 47 minus 36 rechnen, wenn wir 36 +  = 47 lösen wollen. Wir lernen es als einen einzigen Rechenschritt – und verbauen uns ab da den Vorteil der Mathematik. Schlimmer noch, verbauen uns das Verständnis für Mathematik überhaupt.

Die methodische Vorgehensweise ist hier scheinbar überhaupt nicht notwendig, weil die Lösung „offensichtlich“ ist. Und jetzt nehmen Sie bitte folgende Aufgabe: Peter wäscht das Auto seines Nachbarn und bekommt dafür 3 Euro, anschließend kauft er sich ein Buch für 12 Euro und hat danach 17 Euro. Wieviel hatte er vorher?

Bitte rechen Sie das Ergebnis aus. Schreiben Sie jetzt das Ergebnis auf ein Blatt Papier.

Schreiben Sie es bitte jetzt auf.

Stopp: Haben Sie es wirklich ausgerechnet? Schreiben Sie den Zahlenwert bitte auf ein Blatt Papier vor sich und machen Sie sich klar, wie Sie es ausgerechnet haben. (Ok, Sie wollen es nicht aufschreiben. Aber glauben Sie mir: Es macht mehr Spaß, meine Texte auf diese Art zu lesen.)

Ich verrate Ihnen etwas: Diese Aufgabe bringt etliche deutsche gebildete Erwachsene in Schwierigkeiten. Denn sie wenden die Methode an, das Ergebnis durch Nachdenken zu ermitteln. Wenn Peter danach 17 Euro hat und vorher 12 ausgegeben hat, dann muss er irgendwann 12 mehr gehabt haben. Aber er hat drei Euro eingenommen, also muss er diese drei  – ja: mehr? weniger? wovon mehr oder weniger? gehabt haben. Mist. Die erste Zahl wieder vergessen. Nochmal: 17 und 12, äh, addieren, macht 29, dann 3, wie war das, ach ja, abziehen, weil es ja andersherum war als bei der 12, also wovon abziehen, ach ja die 29, also minus 3 also 26. Was war die Frage nochmal? Ach ja: Er hatte vorher 26 Euro. Uff.

Das muss gar nicht mal langsam sein, wenn es klappt (was ein ernstzunehmendes Wenn ist.) Aber ein bisschen peinlich ist das schon, oder? Woran liegt es, dass wir uns hier so anstellen? Die Antwort gibt das Rechenbuch, das wir schon als Kind verwendet haben. Wir sind es seitdem gewohnt, „einfach zu wissen“, wie man ein Ergebnis ausrechnet. Hätte Peter nur ein Buch gekauft und kein Auto gewaschen, wir hätten sofort die fertige Lösung aus der Tasche gezogen und hätten gesagt, klar, einfach die 12 zur 17 addieren und fertig ist die Lösung. Schon in der Schule tausendmal gemacht. Siehe oben. Und deshalb lechzen die Studenten in jeder Vorlesung nach einer „Formelsammlung“, weil sie denken, Mathematik sei das stupide Einsetzen von Zahlen in Formeln, die man sich nicht merken kann, geschweige denn verstehen. Und von denen man für jeden Fall eine eigene braucht.

Aber die einfachste Änderung in der Aufgabenstellung macht die fertige Lösung zunichte. Sie wirft uns zurück in den Stand eines Grundschülers, weil wir ohne die fertige Lösung in der Tasche anfangen müssen zu überlegen. Wir müssen uns den Inhalt der „Rechengeschichte“ (so heißen Textaufgaben heute) klarmachen und dann nachdenken.

Genau hier könnte uns die Mathematik helfen. Sie zeigt uns Methoden, wie wir immer zum Ziel kommen, und zwar ohne zu verstehen, wieso. Mit den scheinbar umständlichen Umformungsregelen der Mathematik wissen wir, dass die Lösung „richtig“ werden muss. Wir können es sogar formal begründen, aber wir könnten und brauchen es nicht inhaltlich zu begründen. Wir brauchen nicht zu begründen, wieso wir die drei Euro von irgend etwas abziehen (versuchen Sie das bitte einmal mit Worten zu erklären). Wir wissen einfach, dass es stimmt. Das heißt formal begründen.

Formal heißt: Wir kennen Regeln, die wir anwenden dürfen, ohne uns jedesmal zu überlegen, was diese Regel inhaltlich aussagt. Was heißt es, wenn ich drei Euro auf beiden Seiten einer Gleichung abziehe? Antwort: nichts; aber es ist richtig. Das ist Mathematik.

Wenn wir in der Grundschule gelernt hätten formal zu arbeiten, dann würden wir ganz anders vorgehen. Wir würden die Aufgabe zuerst in eine systematische Schreibweise übersetzen und schreiben:

? + 3 – 12 = 17

Ab jetzt spielen wir nur noch mit Glasperlen (die hier Symbole heißen) und schieben sie ein wenig hin und her. Übrigens nicht mit den umständlichen Begründungen von dem Beispiel oben, sondern wir schieben sie einfach visuell. Wir wissen jetzt nicht mehr, dass Peter die drei Euro fürs Autowaschen bekommen hat. Wir wissen nur noch, dass wir das Fragezeichen allein stehen haben wollen. Eine einfache Regel zweimal angewendet, schon steht die Lösung da (Regel: Du kannst eine Zahl auf die andere Seite des Gleichheitszeichens schieben, wenn du das Vorzeichen umdrehst):

             ?  =  17 – 3 + 12 = 26

Es macht keinen Sinn, hier erklären zu wollen „wieso“ man 3 abziehen und 12 addieren muss. Es ist einfach richtig. (Man kann das an anderen Stellen hinterfragen, aber hier ist es ein fertiges, visuelles Muster.) Es gibt hier nichts zu verstehen – zumindest nichts Inhaltliches. Jeden Schritt verstehen zu wollen, heißt nichtformal gedacht zu haben. Diese Teile der Mathematik verstehen zu wollen, heißt sie nie verstehen zu können. Wie oft habe ich von meinen StudentInnen schon gehört „Ich verstehe die Mathematik nicht“. Aber das stimmt nicht. Was sie nicht verstehen ist, dass es nichts zu verstehen gibt. Sie denken an Inhalt, wo es um Formen geht.

Ich möchten Ihnen den Unterschied zwischen Form und Inhalt aufmalen. Was sehen Sie unter diesem Absatz? Bitte beschreiben Sie es einmal kurz für sich, bevor sie weiterlesen. Sie haben ja noch von der Rechenaufgabe oben ein Blatt vor sich liegen (das haben Sie doch, oder?). Schreiben Sie dort bitte drei kurze Stichpunkte auf, was Sie hier sehen:

Bitte schreiben Sie die Stichpunkte wirklich auf. Es brauchen ja nur drei Wörter zu sein. Das dauert nicht lange, ich verspreche es Ihnen.

Jetzt sage ich Ihnen, was ich hingemalt habe: Einige senkrechte, waagerechte und diagonale Linien unterschiedlicher Länge und einige gebogene Kurven. Bitte sehen Sie jetzt auf Ihr Blatt: Was haben Sie dort aufgeschrieben? Ist es das, was ich gezeichnet habe? Oder ist es das, was Sie daraus gemacht haben? Ich bin mir fast sicher: Sie haben meine Striche als Stereotype für etwas anderes interpretiert. Dieses Interpretieren ist der Inhalt; meine Linien sind die Form.

Bitte betrachten Sie das Bild noch einmal und bitte betrachten Sie es diesmal rein formal. Bitte zeichnen (nicht schreiben) Sie jetzt auf Ihr Blatt, was Sie sehen. Tun Sie es, bevor Sie weiter herunterscrollen.

 

 

 

 

 

Ist auf Ihrem Blatt jetzt ungefähr folgendes?

Wenn nein: Warum nicht? Höchstwahrscheinlich, weil Sie sich nicht vollständig von den Inhalten gelöst haben. Wie auch immer, sehen Sie die unglaubliche Bereicherung durch die formale Sicht? Sehen Sie, dass Sie auf einmal eine völlig neue Sicht auf etwas scheinbar Altbekanntes haben können? Dass Sie jetzt etwas qualitativ anderes sehen als zuvor? Sehen Sie, dass Sie sich ohne jede Anstrengung von alten Denkmustern lösen können? Das ist Mathematik.

Sie sehen hier auch, dass es in der formalen Sicht ebenso Regeln gibt wie in der inhaltlichen, nur eben andere. Bei meiner Umgruppierung der Linien habe ich die Länge und Richtung der Linien als Unterscheidungsmerkmal angenommen, nicht aber ihre räumliche Lage. Auch habe ich ein Kriterium verwendet, nach dem eine Linie eine eigenständige Linie ist: Sehen Sie die Doppelbögen oben rechts? Ist jeder Doppelbogen eine zusammengehörige Linie oder ist jeder Bogen eigenständig? Das sind formale Regeln. Heben Sie diese Regeln teilweise auf, dann erhalten Sie zum Beispiel folgendes Bild:

Woher kommen die formalen Regeln? Die für Viele erstaunliche Antwort: Wir denken sie uns aus. Kriterien dabei sind oft Ästhetik und Harmonie, manchmal Einfachheit. Nie ist es aber ein Kriterium aus der Welt der Inhalte. Wir haben die Formalwissenschaft erfunden, um uns von den Inhalten lösen zu können. Damit leben wir auf einmal in einer anderen Welt.

Es gibt hier keine Häuser, Menschen und Vögel. Sondern nur Linien; oder Punkte, Linien, Flächen. Mit denen spielen wir nach eigenen Regeln, nach Regeln, die es in der „echten“ Welt unserer Erfahrung nicht gibt, zumindest nicht geben muss. Viele nennen das Abstraktion, aber das trifft es nur zum Teil. Denn Abstraktion klingt so, als sei diese Welt frei von Anschauung oder Vorstellung. Dabei ist das Gegenteil der Fall: Diese Welt ist voller Anschauung, aber einer ganz anderen als in der inhaltlichen Welt. Bitte schieben Sie jetzt noch einmal die Linien auf dem Bild oben ein wenig hin und her. Sehen Sie, dass Sie hier in der Tat sehen? Die formale Vorgehensweise ist hochgradig visuell. Mit Worten beschreiben zu wollen, was Sie hier tun, würde es fürchterlich langsam machen, fürchterlich umständlich und der Sache jeden Spaß nehmen.

Jetzt kommen unser Rechenbuch und unsere Lehrerin. Die beiden erklären uns, dass wir eine Aufgabe wie oben als „Umkehraufgabe“ lösen sollen. Das ist ein Wort – nichts Visuelles. Eine Umkehraufgabe? Aha, wir sollen plus statt minus rechnen und umgekehrt. Aber wo genau? Bei dieser Aufgabe:

A +  ? = B

Und bei folgender?

A – ? = B

Was ist jetzt die Umkehraufgabe? Viel Spaß! Sie lautet:

? = A – B

Das kommt heraus, wenn man eine visuelle Aufgabe verbal lösen will. Es funktioniert nicht. Man müsste schon für die einfachsten Aufgaben Unmengen von Lösungswegen lernen, die alle eigene Namen haben. Dabei würden es etwa fünf einfache, visuelle Verschieberegeln tun.

Diese Unfähigkeit, formal zu denken, hängt den meisten Menschen ihr Leben lang nach. Dadurch bleiben sie auf dem mathematischen Niveau eines Zehnjährigen stehen. Und das nur, weil wir es in der Grundschule gut meinen und „veranschaulichen“ und „erklären“.

Wir „erklären“, indem wir formale Regeln mit Inhalten aus der Erfahrungswelt beschreiben. Wir sagen: „Jetzt hör mal zu, Peter hat doch drei Euro bekommen, deshalb müssen wir sie abziehen, wenn wir wissen wollen, was er vorher hatte“. Abziehen, weil er etwas bekommen hat? Schon richtig, aber es dauert sehr lange, zu verstehen wieso. Und das, obwohl man es gar nicht zu verstehen braucht. In der formalen Welt ist dieser Schritt ein kleiner erlaubter Schritt, den wir flink ausführen, ganz ohne jede Anstrengung. In der Welt der Inhalte und der Erklärungen ist er eine Plage.

Deshalb ist es grundverkehrt, im Mathematikunterricht zu „veranschaulichen“, indem man Inhalte hinzunimmt. Denn die Welt der Inhalte stört hier nur. Statt dessen sollte man die Regeln der formalen Welt veranschaulichen. Wir sollten lehren, wie man mit den Formen spielt, wie man Harmonie in Unordnung bringt, welche Ästhetik in Formen steckt, welche Rolle die Einfachheit spielt, wie man gruppiert, umordnet, verteilt und zusammenfasst. Und das rein formal, durch visuelles Spielen, nicht durch in Worte fassen.

Das ist keineswegs schwierig. Jeder gesunde Mensch kann eine Handvoll einfacher Verschieberegeln lernen und anwenden. Jeder, der versteht, dass es um Spielen geht. Wer denkt, es ginge um Peters drei Euro, die Entfernung zur Schule oder das Alter von Vater, hat verloren.

Erst ganz am Ende sollten wir rückübersetzen: Was war das Kästchen doch gleich? Es war der Betrag, den Peter „vorher“ hatte. Antwortsatz: Peter hatte vorher 26 Euro.

 

Aber wieso hatte Peter vorher 26 Euro? Kannst du mir das erklären? Nein, liebe Lehrerin und liebes Schulbuch, das kann ich nicht erklären. Es ist richtig, weil ich formal alles richtig gemacht habe. Es ist richtig, weil der Satz Hand und Fuß hat und das Ergebnis das gleiche ist wie wenn Sie lange nachdenken. Bitte keine Verwirrungen. Anfang und Ende mögen „echte Welt“ mit Inhalten sein; dazwischen ist Mathematik als reine Form. Nichts zu verstehen, nichts zu erklären.

Ich kenne die Diskussion, ob man Form und Inhalt trennen kann. Ich möchte sie hier nicht aufwärmen, aber ich sage Ihnen eines: Wer Form und Inhalt nicht trennt, kann nicht mathematisch denken. Denn Mathematik ist eine Formalwissenschaft.

 

Häufige Einwände

GrundschullehrerInnen geben sich an dieser Stelle keineswegs geschlagen. Schön und gut, dass Mathematik eine Formalwissenschaft ist, aber dem Kindergehirn fehlt schlichtweg die Reife, eine derartige Abstraktion zu begreifen. Man muss das schon kindgerecht aufbereiten. Sagt doch jedes Pädagogikbuch und jedes Lehrbuch der Entwicklungspsychologie.

Soso. Dann werfen wir mal einen Blick auf die ersten Schreibübungen, die es teilweise bis heute gibt. Dort sehen wir eine Abfolge von verschiedenen bedeutungslosen Zeichen, etwa so (früher hieß so etwas Zierleiste):

////////

///\\\ ///\\\///\\\///\\\///\\\

o-/\-o-/\-o-/\-o

Ist das nicht genau die visuell-formale Welt, von der wir hier gesprochen haben? Und haben Kinder der ersten Grundschulklasse irgendwelche Schwierigkeiten, ein solches Muster zu erkennen und seine Regelmäßigkeit zu erlernen? Natürlich nicht. Schon viel kleinere Kinder können völlig problemlos abwechselnd verschiedenfarbige Duplosteine zusammenstecken oder aneinanderreihen. Weshalb sollte ein Kind der zweiten Grundschulklasse nicht die einfache Regel lernen können, dass man eine Zahl von einer Seite des Gleichheitszeichens auf die andere schieben kann, wenn man dabei das Vorzeichen wechselt? Natürlich kann es das lernen, und zwar völlig problemlos.

Das Problem ist nicht die formale Regel – die ist durchaus kindgerecht. Das Problem ist die „kindgerechte“ Veranschaulichung. Was bedeutet es, dass wir die 3 abziehen? (Dass Peter drei Euro weniger gehabt haben muss, um auf den Endwert von 17 zu kommen. Kindgerecht?) Was bedeutet das Minus vor der Drei? Und – oje – was bedeutet es, wenn davor keine weitere Zahl steht? (Du kannst dir doch drei Euro vorstellen. Jetzt stell dir vor, du hättest sie dir geliehen und musst sie wieder zurückgeben usw. Kindgerechter als: Schiebe die Zahl auf die andere Seite und schreibe ein Minus davor?) Inhalt an der falschen Stelle reißt die Kinder gnadenlos aus der Harmonie der Form.

 

Und jetzt kommt ein sehr cleverer Einwand:

Ich bin mal über Ihre Internetseite gegangen. Dort sehe ich auf jeder Seite fast nur Wörter, kaum mal ein Bild und ganz selten eine Formel. Wenn die formale Seite der Mathematik so harmonisch und leichtverständlich ist, wieso verwenden Sie sie denn dann so wenig? Und wieso erklären Sie so viel mit Worten?

Raffiniert argumentiert. Aber ich habe gute Gegenargumente:

1. Wenn ich hier mehr mit Formeln arbeiten würde, dann würden Sie meine Seite gar nicht erst lesen. Viele Menschen in Deutschland haben eine solche Abscheu vor Mathematik, dass der reine Anschein bereits genügt, nicht ein einziges Wort zu lesen. Ich kenne das, wenn ich Vorträge halte oder Seminare gebe: Eine Formel zur falschen Zeit, und es gibt ein hysterisches Lachen wie bei einer unzensierten Bettszene im Kino. Einfachste Argumente als Formel geschrieben, und der Raum wird tröpfchenweise leer. Deshalb meide ich jeglichen Anschein von Mathematik (sorry: nicht in meinen Vorlesungen, aber schlimm wird’s auch da nicht).
2. Und verwende sie trotzdem. Bitte sehen Sie sich einmal die typische Argumentation an. Ich beschreibe einen Sachverhalt so, dass man ihn danach direkt als Formel aufschreiben kann. Und genau das tue ich dann auch meist direkt danach – schon tut die Formel gar nicht mehr weh. Dann gibt es einige formale Umformungen, die ich aber zur Sicherheit gern in einer Fußnote verstecke. Oder schlichtweg die Ergebnisse nenne, die ich oder andere auf formalem Weg gefunden haben.
3. Und anschließend interpretiere ich das Ergebnis. In diesem Schritt tauchen wir gemeinsam wieder aus der formalen Welt auf und versuchen inhaltlich zu verstehen, was wir (oder andere vor uns) da eigentlich getan haben. Dieser Schritt ist extrem wichtig – ohne ihn wäre angewandte Mathematik vollkommen wertlos. Leider ist das der Schritt, der von den meisten Spieltheoretikern nicht vollzogen wird. Viele von ihnen bleiben auf der rein formalen Ebene (was einen eigenen Charme hat), aber ich sehe meine Aufgabe zum großen Teil darin, diese formalen Ergebnisse mit inhaltlichem Leben zu füllen. Also der Form wieder Inhalt zu geben.

Ich plädiere nicht dafür, Inhalte auszublenden. Sondern ich plädiere dafür, unseren Kindern (und den Erwachsenen) zusätzlich beizubringen, wie man in der formalen Welt lebt. Und wie und an welchen Stellen man die beiden Welten verbindet. Das ist übrigens der Inhalt meiner gesamten Webseite. Ach ja, auch meines Spieltheorie-Buches.