Inhaltsverzeichnis
- Schnick-Schnack-Schnuck und mehr
- Schnick, Schnack, Schnuck, Schnöck: Multi-Knobeln
- Schnick Schnack ohne Schnuck
- Klassen des Knobelns
- Wie sich Stein, Papier und Schere durchdringen: Anti-Transitivität
- Und jetzt die Spieltheorie
- Schnick-Schnack-Schnuck in Normalform
- Knobeln mit Brunnen
- Das spieltheoretische Optimum: die Mischung macht’s
- Spiel-Strategien
- Tarnen und beobachten
- Psychologie und Gambits
25.09.2006 (11.09.2006)
Schnick-Schnack-Schnuck
Papier, Stein, Schere ist ein erstaunliches Spiel, an dem man Vieles über die Spieltheorie und über das echte Leben lernen kann. Und Sie denken, das alles wäre ein Kinderspiel!
Schnick-Schnack-Schnuck und mehr
Kinder lieben es, sich gegenseitig zu ärgern (Erwachsene auch, aber sie verheimlichen es besser). Deshalb führen Kinder gern immer wieder den Brunnen als zusätzliches Symbol ein (am liebsten unangekündigt, aber das fällt schon in die Rubrik „Mogeln“, zu der noch weiter unten kommen). Der Brunnen schlägt Stein und Schere (weil beide hineinfallen können), wird aber vom Papier geschlagen, weil es ihn abdecken kann. Viele Kinder und Erwachsene können sich über diese Regelerweiterung fürchterlich aufregen, weil der Brunnen ja ein unfaires Symbol ist, indem er zweimal schlägt, aber nur einmal geschlagen wird. Es mag sein, dass diese Asymmetrie die Harmonie des Originalspiels stört (ich mag den Brunnen auch nicht), aber die Logik zerstört es keineswegs. Denn solange jedes Symbol mindestens einmal geschlagen werden kann und mindestens einmal schlägt, führt dies zu einer spieltheoretischen Lösung mit einer ähnlichen Struktur wie im Original-Schnick-Schnack-Schnuck. Wie wir unten sehen werden, kann man sogar durch ein wenig Nachdenken die Harmonie des Originalspiels wieder herstellen. Ein Glück.
Schnick, Schnack, Schnuck, Schnöck: Multi-Knobeln
Geht das Knobeln eigentlich auch mit mehr als drei Symbolen? Natürlich ja, prinzipiell gehen beliebig viele. Zum Beispiel hat sich ein netter Mensch namens David Lovelace die Mühe gemacht, sich eine 25-Symbol-Version des Knobelns auszudenken. Er hat auch die 7-, 9- 11- und 15-Zeichen-Knobel-Version im Angebot. Die Spielbarkeit mag eine separate Frage sein, aber von der Logik her kann er sich den Rest seines Lebens mit der Entwicklung weiterer n-Knobel-Varianten beschäftigen. (Viele Kinder fangen damit schon auf dem Schulhof an und entwickeln die verrücktesten Knobel-Gebilde. Ob sich das lohnt schreibe ich später noch einmal, damit Sie einen Grund haben wiederzukommen.)
Natürlich muss man noch ein paar kleine Gedanken darauf verwenden, wann Knobeln noch Knobeln ist. David Lovelace’s Definition besteht darin, dass jedes Symbol genauso oft geschlagen werden muss, wie es selbst schlägt (nun gut, er betrachtet sich als Künstler, nicht als Mathematiker, daher nennt er dies keine Definition, und wie Künstler nunmal so sind, spricht er noch nicht einmal die Definition überhaupt aus; aber er setzt sie stillschweigend voraus, und das ist im Resultat eben eine Definition. Welt wieder in Ordnung.). Jedenfalls ist diese Definition nicht ganz unsinnig. Denn, wie wir schon beim Beispiel mit dem Brunnen gesehen haben, gehen zwar prinzipiell auch andere Varianten, in denen ein Symbol mehr als die anderen schlägt. Aber (und das hat David auch entdeckt) fällt in diesem Fall das Spiel wieder zurück auf eine einfachere Variante mit einer ungerade Anzahl Symbolen (die aber nicht immer nur drei sein muss). Grund dafür ist eine Dominanzbeziehung zwischen den Strategien (Symbolen), aber dazu später.
Daher entwickelt er auch keine geradzahligen Schnick-Schnack-Schnuck-Varianten, weil dort grundsätzlich einige Symbole seltener schlagen müssten als andere. Allerdings wird er hier Opfer seiner Definition, die er nicht aufgeschrieben hat. Denn offenbar setzt er nicht nur voraus, dass jede Strategie gleich oft schlagen und geschlagen werden muss, sondern auch, dass bei allen Kombinationen aus ungleichen Strategien eine schlägt und eine geschlagen wird. Machen wir das an einem Beispiel und basteln uns ein Schnick-Schnack-Schnuck mit Feuer, Schwamm, Luft und Wasser. Wann immer zwei verschiedene Symbole gezeigt werden, muss eines gewinnen und das andere verlieren – wenn das die Voraussetzung ist, dann muss durch die gerade Anzahl mindestens eines der Symbole weniger oft gewinnen als die anderen und damit muss mindestens eines der Symbole (nach einigen schlauen Überlegungen) wegfallen. Aber Vorsicht: Es fallen nicht etwa automatisch alle Symbole weg, die seltener gewinnen. Weshalb das so ist, das sehen Sie hier.
Wenn wir aber – abweichend von Davids heimlicher Definition – manchmal ein Unentschieden zulassen (was wir bei zwei gleichen Symbolen ja auch akzeptieren), dann können wir wieder Waffengleichheit herstellen. Zum Bespiel gewinnt dann Feuer gegen Schwamm gegen Luft gegen Wasser gegen Feuer und alle anderen Kombinationen sind unentschieden. Also wäre dann Feuer gegen Luft ebenso unentschieden wie Feuer gegen Feuer. Wie gesagt – die Spielbarkeit lassen wir einmal außer acht.
Hier das Schnick-Schnack-Schnuck-Schnöck mit vier Strategien, von denen keine dominiert ist – ich werde Ihnen in der Zukunft noch einmal zeigen, wieso das ein wichtiger Fall ist:
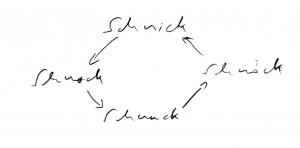
Und hier das Schick-Schnack-Schnuck-Schnöck-Schnäck, bei dem nur gleiche Würfe zu einem Unentschieden führen und keine Strategie dominiert ist (ich erkläre weiter unten, was das ist), da die Strategienzahl ungerade ist:

Also gut, bei David Lovelace sind die Bilder schöner – dafür hat er an das erste nicht gedacht. Hier sein RPS-25 (Rock, Paper, Scissors 25), das er Ihnen auch gern auf einem T-Shirt verkauft:

Nach einem Blick auf dieses wundervolle Bild sieht man auch, dass es gar nicht so schlimm ist, wenn man bei jedem Symbol noch ein Unentschieden zulassen würde. Bei den 25 möglichen Symbolen der Gegenspielerin gäbe es dann eben zweimal unentschieden, nämlich einmal, wenn sie dasselbe Symbol wirft wie man selbst, und ein anderes Mal, wenn sie das gegenüberliegende wirft. (Man kann die Symbole o.B.d.A. so anordnen, dass das genau so gilt.) Bei sechs Symbolen sieht das das dann so aus:
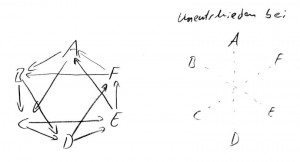
Schnick Schnack ohne Schnuck
Wenn wir schon einmal dabei sind, dann können wir uns auch gleich die Frage stellen, ob Knobeln nicht auch mit weniger als drei Symbolen geht. Die einfache Antwort lautet: kommt drauf an. Nämlich darauf, wie weit wir bereit sind, zu abstrahieren. Für ein Spiel mit spieltheoretisch sehr ähnlicher Lösung ginge auch Schnick-Schnack, Schnuck kann man weglassen. In der spieltheoretischen Lehrbuchliteratur gibt es sogar ein Spiel, das exakt diese Struktur hat und das ich zum Beispiel auch in meinem Spieltheorie-Lehrbuch verwende, um gemischte Strategien zu erklären. Es ist das Spiel matching pennies, das den Grundtyp des Diskoordinationsspiels darstellt. (Jede Form von Knobeln ist ein Diskoordinationsspiel, aber dazu später.) Bei matching pennies legen zwei Spieler einen Pfennig zunächst verdeckt vor sich auf den Tisch und decken ihn dann gleichzeitig auf. Spieler Anton hat gewonnen, wenn bei beiden Spielern die gleiche Seite nach oben zeigt, Spielerin Berta hat gewonnen, wenn unterschiedliche Seiten nach oben zeigen. Man kann dieses Spiel auch zu einem Handspiel verwandeln (das dann manchmal Gerade-Ungerade genannt wird): Wie bei Stein, Schere, Papier zeigen die Spieler gleichzeitig entweder einen oder zwei Finger (um Missverständnissen vorzubeugen empfiehlt es sich, bei einem Finger nicht den Mittelfinger zu nehmen). Wenn die Anzahl der Finger gerade ist, dann gewinnt Anton, wenn sie ungerade ist, gewinnt Berta.
Bei der Betrachtung der spieltheoretischen Lösung sieht man, dass diese in der Tat gleichartig ist wie bei Stein, Papier, Schere. Unterschiedlich ist aber, dass hier nicht jedes Symbol (also die beiden Seiten des Pfennigs bzw. die Anzahl der Finger) je einmal schlägt und geschlagen wird, dass also keine intransitive Beziehung zwischen den Symbolen vorliegt (auf die ich auch gleich noch eingehe).
Geht es mit noch weniger Symbolen? Wie steht es zum Beispiel um das einfache Werfen einer Münze? Ist das auch noch Knobeln? Wie so oft in der Mathematik ist das natürlich eine Frage der Definition, aber ich würde dieses einfache Münze werfen klar als etwas anderes ansehen als Knobeln in seinen verschiedenen Varianten. Denn beim Knobeln wählt jeder Spieler eine Strategie und deren Zusammentreffen bestimmt den Spielausgang. Mag sein, dass das zu einem „Glückspiel“ wird, mag sein, dass hier der Zufall früher oder später eine wesentliche Rolle spielt. Aber zunächst handelt es sich um eine eindeutige Entscheidung jedes Spielers, für die er keinerlei Zufall braucht. Im Gegensatz dazu treffen die Spieler beim Münze werfen überhaupt keine Entscheidung, sondern es gibt nur einen einzigen Zufallszug. Daher ist das Spiel von seiner strategischen Natur her etwas ganz anderes (selbst, falls es im Resultat auf das gleiche hinausläuft, was allerdings erst noch zu zeigen ist).
Klassen des Knobelns
Als Professor kann ich hier nicht widerstehen: Ich muss diese Typen von Spielen einfach klassifizieren. Und zwar so:
Losentscheidungen (Nur der Zufall entscheidet – also spieltheoretisch kein echtes Spiel, sondern eine Lotterie)
Knobeln (Die Spieler entscheiden über reine Strategien)
Allgemeine Diskoordinationsspiele
Intransitiv angeordnete Symbole vom Typ Schere, Stein, Papier
Ob das etwas bringt, sei mal dahingestellt. Aber wenigstens verstehen wir jetzt schon einige der subtilen Unterschiede zwischen den Spieltypen.
Wie sich Stein, Papier und Schere durchdringen: Anti-Transitivität
Die Symbole beim Schnick-Schnack-Schnuck stehen offenbar in einer Beziehung zueinander, nämlich es schlagen einige andere und werden von einigen anderen geschlagen. In der Mathematik heißen derartige Beziehungen „Relationen“.
Auch im Alltag sind wir gewohnt mit Relationen umzugehen, zum Beispiel mit Ordnungsrelationen. Daher sind wir es gewohnt, dass wir Gegenstände in eine „natürliche“ Ordnung bringen können. Also zum Beispiel: Ich mag lieber Kaugummieis als Pistazieneis; zudem mag ich lieber Pistazieneis als Schokoladeneis. Wenn Sie mich jetzt zum Eis einladen und es nur Kaugummieis und Schokoladeneis gibt, dann wissen Sie dennoch schon, dass ich bei dieser Auswahl lieber Kaugummieis mag, obwohl ich Ihnen für dieses Paar noch gar nicht meine Vorliebe gesagt habe. Sie erschließen das aus der Tatsache, dass jemand, der Kaugummieis lieber mag als Pistazieneies und dieses lieber als Schokoladeneis, dass dieser Jemand also Kaugummieis erst recht lieber haben muss als Schokoladeneis. Meine Vorliebe geht sozusagen durch das mittlere Eis hindurch. Dieses Hindurchgehen heißt in halbem Latein „Transitivität“ und ist ein Merkmal einer jeden Ordnungsrelation. Ohne Transitivität keine Reihenfolge.
Und damit sind wir beim Stein-Papier-Schere-Spiel: Die Symbole sind hier intransitiv angeordnet, genauer gesagt, anti-transitiv. Wenn die gleichen Regeln beim Eisessen gelten würden, dann würde ich beim Vergleich von Kaugummi- und Schokoladeneis das Schokoeis bevorzugen. Das mag beim Eisessen nicht sinnvoll sein, aber Schnick-Schnack-Schnuck ist ein Spiel, dessen Regeln anfangs frei bestimmen werden konnten. Und der Erfinders des Spiels hat sich hier eben etwas ausgedacht, was uns verwirren sollte – was es zweifellos auch tut, weil die Symbole eben keine Ordnungsstruktur aufweisen, sondern anti-transitiv zueinander sind.
Diese Antitransitivität ist also das Kernstück des Knobelns. Sehen wir uns jetzt die spieltheoretische Lösung an.
Und jetzt die Spieltheorie
Schnick-Schnack-Schnuck in Normalform
Bei Zweipersonen-Spielen ist es oft die übersichtlichste Art, alle Strategien in einer Tabelle (also einer Matrix) anzuordnen, und zwar so, dass alle Kombinationen der beiden Spieler sichtbar sind. Für Schnick-Schnack-Schnuck sieht das dann so aus:
| Berta | ||||
| Stein | Papier | Schere | ||
| Stein | 0 | -1 | +1 | |
| Anton | Papier | +1 | 0 | -1 |
| Schere | -1 | +1 | 0 |
Jeder Spieler wählt gleichzeitig mit dem anderen eines der drei Symbole. Wir nennen hier jedes Symbol eine Strategie. Und müssen gleich ein wenig aufpassen, weil ernsthafte Schnick-Schnack-Schnuck-Spieler es vermutlich eher als Strategie bezeichnen würden, welche Abfolge von Symbolen sie wählen (die Vollprofis nennen das Gambits). Aber verwenden wir hier ruhig die in der Spieltheorie übliche Bezeichnung.
Wie soll man sich in diesem Spiel verhalten? Die Frage ist nicht ganz so leicht zu beantworten, weil die drei Symbole eben in anti-transitiver Beziehung zueinander stehen. Das sieht man daran, dass in jeder Zeile und in jeder Spalte einmal –1, einmal +1 und einmal 0 steht. Diese Zahlen sind die Auszahlungen an Anton: +1 heißt, er hat Berta geschlagen, -1 heißt, sie hat ihn geschlagen, 0 heißt Unentschieden. Weil dieses Spiel ein Nullsummenspiel ist, reicht es, wenn wir die Auszahlungen an Anton aufschreiben – Berta bekommt immer das gleiche mit umgedrehtem Vorzeichen, sprich: sie verliert, was er gewinnt und umgekehrt. Genau das ist übrigens das Kennzeichen eines Nullsummenspiels.
Knobeln mit Brunnen
Bevor wir uns an die Lösung dieses Spiels machen, werfen wir noch einen Blick auf die Knobel-Variante mit Brunnen. Nicht um Sie zu verwirren, sondern weil wir dort eine sehr einfache (Teil-) Lösung finden können:
| Berta | |||||
| Stein | Papier | Schere | Brunnen | ||
| Stein | 0 | -1 | +1 | -1 | |
| Anton | Papier | +1 | 0 | -1 | +1 |
| Schere | -1 | +1 | 0 | -1 | |
| Brunnen | +1 | -1 | +1 | 0 | |
Die schöne Eleganz des Original-Knobelns ist hier zunächst einmal weg (so sind sie, die Kinder). Statt der harmonischen Symmetrie gewinnt jetzt Brunnen zweimal und Schere und Stein verlieren zweimal. Aber ein wenig Nachdenken bringt die ursprüngliche Eleganz zurück. Vergleichen Sie bitte einmal die Strategien Stein und Brunnen aus Sicht von Anton. Wenn Berta Papier oder Schere wirft, dann sind Stein und Brunnen für Anton gleich gut. Wirft Berta Stein oder Brunnen, dann ist es für Anton besser Brunnen zu werfen als Stein. Mit anderen Worten: Brunnen ist nie schlechter als Stein, aber manchmal besser. Genau das ist die Definition der dominierten Strategie: Brunnen dominiert Stein. Zur Übung können Sie das auch aus Sicht von Berta noch einmal machen, und Sie werden sehen, dass Brunnen auch aus ihrer Sicht Stein dominiert (denken Sie aber daran, dass für Berta die Vorzeichen der Auszahlungen umgedreht sind).
Folglich können beide Spieler die Strategie Stein streichen – es ist niemals rational, sie zu wählen. Wenn nun beide Stein streichen, dann bleibt folgendes Spiel übrig:
| Berta | ||||
| Papier | Schere | Brunnen | ||
| Papier | 0 | -1 | +1 | |
| Anton | Schere | +1 | 0 | -1 |
| Brunnen | -1 | +1 | 0 |
Und was sehen wir? Das Original-Schnick-Schnack-Schnuck ist wieder da, nur dass hier Stein durch Brunnen ersetzt wurde. Vorausgesetzt natürlich, die Spieler kommen gedanklich so weit, dass sie einfach Stein streichen können – aber das tun rationale Spieler natürlich. Und andere gibt es hier nicht, schließlich leben wir in der Welt der Mathematik, sprich: in der Spieltheorie und nicht in der Spielpraxis (die kommt später dran). In der Spieltheorie musste jetzt jedenfalls der Stein weichen, weil der Brunnen dazukam. Die Schere durfte bleiben, weil sie zwar auch nur einmal gewinnt, aber sie dann gewinnt, wenn es der Brunnen nicht tut. Ungerecht, aber so ist es nun mal.
Das hilft uns natürlich noch nicht beim Originalspiel weiter, denn von den drei Strategien ist keine dominiert. Daher ist es zunächst einmal nicht nichtrational, jede von ihnen potenziell zu wählen. (Genau: Wenn etwas nicht nichtrational ist, dann ist es noch lange nicht rational; aber ein bisschen mehr rational als nichtrational. Sorry, ich schweife ab …).
Das spieltheoretische Optimum: die Mischung macht’s
Sehen wir uns einmal etwas an, was definitiv nicht rational ist. Das wäre zum Beispiel die Vorgehensweise immer Stein zu spielen. Nehmen wir einmal an, es wäre rational, immer Stein zu werfen. Dann würde der andere seine beste Antwort darauf wählen, und die lautet Papier. Wenn ich also ganz fest daran glaube, dass es rational ist, Stein zu werfen, dann weiß ich, dass der andere Papier wählen wird. Wenn ich aber das weiß, dann wähle ich Schere. Daher zerstört sich der Glaube an die Rationalität von „immer Stein“ aus sich selbst heraus – es kann nicht rational gewesen sein (das ist die Beweisführung der reductio ad absurdum, die ich liebe). Es hilft auch nichts, dann eben immer Schere zu werfen, denn dann wählt der andere immer Stein und ich immer Papier und er immer Schere usw. So kommen wir nicht weiter.
Das Problem ist, dass es zu jeder Strategie, die vorhersehbar ist, eine Gegenstrategie gibt, die gewinnt. Daher brauchen wir eine Strategie, die unvorhersehbar ist. Unvorhersehbar ist aber nur ein anderes Wort für zufällig. Also muss die Strategie zufällig sein. Sie muss zufällig eine der drei „reinen Strategien“ auswählen – das nennt man eine gemischte Strategie.
Aber nicht jede gemischte Strategie ist rational. Wenn wir zum Beispiel ein bisschen zu oft Stein wählen, dann kann uns unser Gegner leicht über den Tisch ziehen, indem er ein bisschen zu oft Papier wählt. Genau das ist übrigens der Punkt, an dem die Schnick-Schnack-Schnuck-Meister einsetzen (ja, es gibt hier sogar Weltmeisterschaften). Aber bleiben wir zunächst bei den vollständig rationalen Spielern aus der Welt der Mathematik, deren Verhalten wir hier erst einmal als Referenzpunkt bestimmen wollen.
Wie errechnen wir die Wahrscheinlichkeiten für das Nash-Gleichgewicht? Das ist leider ein bisschen komplexer, aber ich kann Ihnen das Prinzip verraten: Sie stellen eine Gleichung auf, die Ihre Auszahlung in Abhängigkeit von Ihrer Wahrscheinlichkeit und der Ihres Gegenspielers beschreibt. Dann maximieren Sie diese Funktion nach Ihrer Wahrscheinlichkeit. Das bringt Sie zu einem Gleichungssystem mit drei Unbekannten (nämlich den Wahrscheinlichkeiten für jede reine Strategie), das Sie lösen können. Wer es genauer wissen will, der braucht mein Spieltheorie-Buch – alle anderen können mir einfach einmal glauben, dass hier tatsächlich ein Mischungsverhältnis herauskommt, bei der man jede reine Strategie mit einer Wahrscheinlichkeit von 1/3 wählt. Mit anderen Worten: Im Gleichgewicht ist Papier, Stein und Schere jeweils mit exakt derselben Wahrscheinlichkeit zu wählen.
Wohlgemerkt im Gleichgewicht. Damit meine ich natürlich das Nash-Gleichgewicht in gemischten Strategien. Ich wäre aber vorsichtig damit, diese Gleichgewichtsstrategie als eine „optimale“ Strategie zu bezeichnen. Ob sie tatsächlich optimal ist, hängt davon ab, was der Gegenspieler macht. Ist er unglaublich intelligent und sind wir es auch, und wissen wir das auch beide, und wissen auch, dass wir das wissen usw., dann – ja dann kommen wir am Nash-Gleichgewicht kaum vorbei. Aber ist unser Gegner nicht so neunmalklug, oder wissen wir nicht, ob er es ist, oder wissen wir nicht, ob er weiß, dass wir es sind oder oder – dann kann eine Abweichung vom Gleichgewicht rational sein.
Aber wohin sollen wir abweichen? Wenn wir zwar eine Vermutung haben, unser Gegner könne von der Gleichgewichtslösung abweichen, wissen aber nicht, in welche Richtung, dann ist es schon wieder zufällig. Und indem er abweicht, verschafft er zwar uns die Möglichkeit, ihn auszubeuten, aber indem wir versuchen, ihn auszubeuten, werden wir selbst ausbeutbar, weil wir ja abweichen. Und genau das bringt uns wieder zurück zum Gleichgewicht. Man kann sogar weitergehen: Indem jeder Spieler glaubt, er sei schrecklich schlau und würde den anderen ausbeuten, macht er Dinge, die de facto den Zufall simulieren. Sie sind vielleicht nicht zufällig, wenn er seine eignen Gedanken zugrunde legt. Aber die Resultate sind es. Und damit verhält er sich so, als ob er zufällig mischen würde. Für uns ist es egal, ob er glaubt, frei zu entscheiden und etwas Zufälliges herauskommt oder ob er wirklich zufällig spielt. Und eines steht fest: Indem wir zufällig mischen, und zwar im Gleichgewichtsmischungsverhältnis, sind wir nicht ausbeutbar. Aber wir können auch nicht den anderen ausbeuten.
Und was kommt heraus? Im Resultat haben beide Spieler eine Wahrscheinlichkeit von 50% zu gewinnen. Das ist so gut wie Münzenwerfen – aber der Weg dahin ist ein völlig anderer. Beim Münzwurf ist es ein Zufallsereignis, das entscheidet. Bei Schnick-Schnack-Schnuck sind es Überlegungen darüber, was rational ist, die die Spieler versuchen lassen, den Zufall ins Spiel zu bringen; oder die sie Überlegungen anstellen lassen, die aus der Sicht eines Dritten aussehen wie Zufall. Das Ergebnis mag das gleiche sein, der Weg dahin ist grundverschieden.
Genug gelesen. Spielen Sie doch einmal selbst Schnick-Schnack-Schnuck und erleben Sie, wie schnell sie ausbeutbar werden; merken Sie, wie dieses Programm auf Sie reagiert? Vergleichen Sie das einmal mit dem trashigsten Schnick-Schnack-Schnuck im Internet, das anscheinend stur die spieltheoretische Lösung spielt, auch wenn Sie offensichtlich davon abweichen (obwohl mir die Grafik ja irgendwie besser gefällt als bei der Version davor). Vielleicht lädt Sie das ein, doch ein wenig mehr über psychologische Spielstrategien zu erfahren. Und falls Sie es zuvor noch komplizierter haben wollen, dann versuchen Sie die Flash-Version von RPS-25.
Spiel-Strategien
Tarnen und beobachten
Einige Spieler schwören darauf, Ihren Wurf von Papier oder Schere zu tarnen. Das tun sie, indem sie bis zum allerletzten Moment so tun, als bliebe es bei Stein. Das funktioniert offenbar bei Gegnern, die in der Lage sind, aus der Handbewegung den zukünftigen Wurf abzulesen. Wenn ein solcher Gegner glaubt, Stein zu sehen, dann wirft er Papier und man gewinnt, indem man im allerletzten Moment aus dem Stein noch Schere macht. Das Tarnen gibt es auch in anderen Varianten, zum Beispiel dem absichtlichen Zucken von Fingern, dem Durchlaufen mehrerer Symbole bis man bei einem stehen bleibt usw. Immer mit dem Ziel, einen Gegner irrezuführen oder wenigstens zu verwirren, der die Hände beobachtet.
Widerspricht das eigentlich der spieltheoretischen Lösung? Keineswegs. Denn es ist eine Variation des Spiels. In dem Spiel, das wir spieltheoretisch gelöst haben, war es eine Regel, dass alle Spieler exakt gleichzeitig ziehen. Diese Regel ist hier aber auf einmal aufgebrochen, zumindest teilweise. Hier hat einer der Spieler die Möglichkeit, den zukünftigen Zug mit überzufälliger Genauigkeit vorherzusagen und der andere Spieler hat die Möglichkeit, diese Vorhersage zu stören. Das ist aber ein neues Spiel, diesmal mit den Vorhersagen und den Störungen als Strategien. Aber es ist eben nicht mehr das Spiel, das wir oben gelöst haben, daher brauchen wir uns auch nicht zu wundern, wenn die Lösung nicht mehr passt.
Bei echten Spielern laufen Bewegungen oft in Gruppen ab. Daher gibt es Bewegungen, die immer bestimmten Würfen vorausgehen (sagen wir ein Ohrenwackeln vor Schere). Die Kunst besteht darin, dies bei seinem Gegner zu entdecken und bei sich selbst zu unterdrücken. Und natürlich kann man falsche Signale einsetzen, um den Gegner glauben zu machen, man habe sich verraten, nur um im entscheidenden Moment doch etwas anderes zu tun. Das ist so ähnlich, wie einige Zeit absichtlich eine Strategie zu häufig zu wählen, um es dann im entscheidenden Moment nicht zu tun. Oder eben doch, weil man denkt, der andere denkt… Vielleicht ist es doch wieder Zufall?
Was könnte man übrigens tun, um solche Komponenten wieder aus dem Spiel zu beseitigen? Eine Regeländerung, mit der man Schummeln durch falsches Timing beseitigt, besteht darin, dass man die Spieler das Symbol hinter ihrem Rücken werfen lässt, sodass es der Gegenspieler nicht sehen kann. Dann können die Würfe auch durchaus zu unterschiedlichen Zeitpunkte erfolgen. Was eine gute Art ist, den Begriff der Gleichzeitigkeit in der Spieltheorie zu verstehen: Gleichzeitig heißt dort nämlich gar nicht immer, dass die physikalische Zeit gleich sein muss, sondern es genügt, dass alle Spieler entscheiden, ohne die Entscheidung des Gegenspielers zu kennen. Diese Methode kann sogar „gleichzeitiger“ sein als der Versuch, den Zug wirklich zu gleicher physikalischer Zeit erfolgen zu lassen.
Psychologie und Gambits
Den verschiedenen Symbolen werde gern Charaktereigenschaften zugeordnet. Zum Bespiel gilt Stein als aggressiv, während Papier eher sanft sein soll. Daher kann es sein, dass ein Spieler, der sich gerade ärgert zu verlieren, eher Stein wirft als Papier. Oder den anderen glauben machen will, dass er sich ärgert und deshalb eher Stein wirft als Papier, weil er in Wahrheit Schere werfen will.
Wie passen derartige Vorgehensweisen eigentlich zur spieltheoretischen Lösung? Sie passen gut, denn sie ändern die Lösung zunächst einmal nicht. Das eine ist die Lösung, das andere ist die Umsetzbarkeit. Das Nash-Gleichgewicht in gemischten Strategien sagt, dass wir völlig zufällig und gleichmäßig mischen sollen. Das ist die eine Sache. Die andere ist, ob wir das können. Und es zeigt sich, dass echte Menschen sehr schlecht darin sind, „wirklich“ zufällig zu mischen. So, wie wir nicht lange Zeit exakt geradeaus gehen können (weshalb wir uns in der Wüste oder auf dem Meer ohne Kompass immer verirren würden) so können wir nicht auch annähernd zufällige Entscheidungen treffen. Wenn wir es versuchen und ein Gegenspieler unsere Abweichungen vom Zufall kennt, dann kann er uns problemlos ausbeuten.
Was kann man dagegen tun? Am besten, man bastelt sich einen echten Zufallsmechanismus (ein normaler Würfel tut es meistens). Leider darf man den während eines Schnick-Schnack-Schnuck-Spiels nicht verwenden. Aber vorher. Wie wir oben gesehen haben, ist der physikalische Zeitpunkt völlig unbedeutend, sofern der Gegenspieler die Entscheidung nicht kennt. Man kann daher völlig problemlos vor dem Spiel auslosen oder auswürfeln, welche Würfe man im echten Spiel nehmen wird. Und schon spielt die Psychologie wieder keine Rolle mehr.
Diese Vorgehensweise wird übrigens unter den Meister-Spielern (oder sind es nur Meisterschafts-Spieler?) als die größte Neuerung im Schnick-Schnack-Schnuck-Spiel gefeiert. Man nennt einen solche vorher festgelegte Abfolge Gambits. Und schon ist die Wahl der Strategie wieder zufällig geworden. So dumm ist das Nash-Gleichgewicht eben gar nicht, stimmt’s?
(Ob das die Herrschaften auf der Schnick-Schnack-Schnuck-Weltmeisterschaft auch wissen?)
In Bremen haben wir das Spiel „Hau, Pieks, Kapu“ genannt. Ich bin der buchstabierung nicht ganz sicher.
Kann keine Referenz dazu finden. Haben Sie das schon mal gehoert?
Danke