Version vom 25.09.15
Erstversion vom März 2006
Immer wieder werde ich gebeten, doch einfach die wichtigsten Grundbegriffe der Spieltheorie zusammenzustellen und kurz zu erklären. Also mache ich mich an die Arbeit: Im Laufe der Zeit werde ich hier immer mehr Konzepte und Begriffe der Spieltheorie hinzufügen.
Die Begriffe stehen in alphabetischer Reihenfolge. Dabei bemühe ich mich zu erklären, was die Begriffe inhaltlich tatsächlich bedeuten und nicht nur, wie ihre mathematische Darstellung ist. Um etwas in diesem Dokument zu suchen, verwenden Sie einfach die Suchfunktion Ihres Browsers (ctrl-f), um meine ganze Seite zu durchsuchen, verwenden Sie die Google-Suche oben.
Wenn Sie mehr über die Begriffe wissen wollen, dann brauchen Sie natürlich mein Spieltheorie-Buch😉
Agent (1) [spieltheoretisches Konzept]
Von Reinhard Selten entwickeltes philosophisches Konzept, demzufolge die Spieler keine durchgehende Identität haben, sondern jede Entscheidung von einem einzelnen Agenten verwaltet wird. Mehrere dieser Agenten können zwar einen natürlichen Spieler darstellen, da die Agenten aber unabhängig voneinander agieren, ist der natürliche Spieler in diesem Konzept eine weitgehend willkürliche Einheit.
Die Konzeption des Agenten beseitigt logische Probleme der Rückwärtsinduktion, die dem Lösungskonzept der Teilspielperfektheit zugrunde liegt. Insbesondere macht es die Vorwärtsinduktion unmöglich, weil im Spielablauf spätere Agenten von den Vorgängern desselben persönlichen Spielers unabhängig agieren.
Der Agent darf nicht mit den -> Typen eines Spielers verwechselt werden.
Agent (2) [Principal-Agent-Theorie]
Die Principal-Agent-Theorie befasst sich mit Situationen, in denen eine Person eine andere beauftragt, etwas zu tun. Klassisches Beispiel ist die Unternehmensinhaber-Manager-Beziehung. In dieser Beziehung ist der Ausführende der Agent, der Beauftragende ist der Principal.
Agentennormalform
Darstellung eines Spiels in der Normalform, bei der die Spieler nicht die persönlichen Spieler sind, sondern die Agenten (1) der Spieler.
Auszahlung
Auszahlungen sind eine Metapher dafür, wie gut die einzelnen Spieler die verschiedenen Spielausgänge finden (Ökonomen sagen dazu: wie die Präferenzordnung der Spieler über die Spielausgänge ist). Mathematisch gesehen erfolgt die Auszahlung in Nutzenwerten, der auf einer Verhältnisskala gemessen werden kann. Das heißt, nicht nur die Reihenfolge der Nutzenwerte hat eine Bedeutung, sondern auch der Abstand der Werte zueinander. Lediglich der Nullpunkt ist willkürlich.
Allerdings hat es sich heutzutage – besonders in den Wirtschaftswissenschaften – eingebürgert, die Auszahlungen als Geldauszahlungen zu interpretieren, was zu vielen Missverständnissen führen kann und manchmal auch schlichtweg unsinnig ist. Der Hauptunterschied zwischen Geldauszahlungen und Auszahlungen in Nutzenwerten besteht darin, dass der Nutzen auch nicht-materielle Entlohnungen enthalten kann (wie soziale Anerkennung, Einhalten moralischer Standards, Freude über die Freude Anderer usw.) und dass die -> Nutzenfunktion so konstruiert ist, dass man bezüglich der Nutzenwerte immer -> risikoneutral ist (siehe auch -> Risiko-Nutzen-Funktion).
Die Auszahlungen sind immer eine individuelle Einschätzung.
Bertrand-Wettbewerb, Bertrand-Oligopol
Ein Bertrand-Oligopol beschreibt den Fall, dass die Oligopolisten den Preis für ihr Gut festsetzen und nicht, wie im -> Cournot-Fall, die Menge. Weil es sich um ein homogenes Gut handelt, kaufen die Konsumenten dann ausschließlich bei dem billigeren Anbieter, andere Anbieter geht leer aus. Wenn gleichzeitig zu diesem Preiswettbewerb keine Kapazitätsbeschränkung des Angebots vorliegt, dann unterbieten sich die Oligopolisten solange gegenseitig, bis sie bei einem Nullgewinn ankommen, selbst dann, wenn sie hierbei noch nicht einmal ihre Fixkosten decken können. Nach diesem Modell haben die Anbieter in einem Oligopol also genauso wenig Marktmacht wie die Anbieter bei vollständiger Konkurrenz.
Das Modell stammt von dem französischen Mathematiker Joseph Betrand, der es im Jahr 1883 als Kritik an dem Oligopolmodell von -> Cournot vorgebracht hat (Joseph Bertrand 1883: Théorie Mathématique de la Richesse Sociale. Journal des Savants 499-508).
Diese Situation ist durchaus realistisch für Branchen, in denen das Gut beliebig vervielfältigt werden kann, also zum Beispiel Software oder Medien, oder auch wenn die Auslastung deutlich unterhalb der Kapazitätsgrenze liegt, zum Beispiel bei Fluggesellschaften oder Hotels außerhalb der Saison. Dagegen führt ein Preiswettbewerb in Branchen mit Kapazitätsbeschränkung prinzipiell zur gleichen Situation wie im Mengenoligopol (also dem Cournot-Oligopol), indem in einer ersten Spielstufe die Kapazität (= Menge) festgesetzt wird, und in einer zweiten Spielstufe zwar ein Preiswettbewerb stattfindet, sich die Konkurrenten aber nicht beliebig weit unterbieten, weil sie durch die Kapazitätsbeschränkung nicht die ganze Nachfrage bedienen könnten, die sie durch den niedrigeren Preis schaffen.
beste Antwort, beste Erwiderung
Eine Strategie ist eine beste Antwort auf das Verhalten der Gegenspieler, wenn sie zur höchstmöglichen Auszahlung führt, die der Spieler dann erreichen kann. Wichtig ist, dass eine beste Antwort nicht eindeutig sein muss: Oft sind mehrere Strategien gleichzeitig beste Antwort.
Coopetition
Coopetition ist eine Wortschöpfung aus co-operation und competition (also Kooperation und Konkurrenz). Coopetition beschreibt die Gleichzeitigkeit beider Prinzipien, die im Geschäftsleben untrennbar verbunden sind. Spieltheoretisch handelt es sich dabei um besondere Fälle der Nicht-Nullsummenspiele, deren extremste Form das Win-Win-Spiel ist.
Cournot-Wettbewerb, Cournot-Oligopol
Das Cournot-Oligopol behandelt den Fall, in dem die Oligopolisten die Menge festsetzen, die sie anbieten, und nicht den Preis. Als Resultat ergibt sich, dass sie zwar einen Mehrgewinn gegenüber der vollständigen Konkurrenz machen, aber weniger als im Monopol.
Trotz der etwas unrealistisch erscheinenden Annahme der Mengenfestsetzung beschreibt das Modell recht gut den Fall für Branchen, in denen die Kapazität nicht kurzfristig geändert werden kann; andernfalls gelten eher die Bedingungen des -> Bertrand-Wettbewerbs.
Das Oligopolmodell von Cournot gilt heutzutage als eine der ersten spieltheoretischen Analysen. Die von Cournot vorgeschlagene Lösung ist ein Nash-Gleichgewicht des Cournot-Spiels.
Cover story
Zu Spielen wird oftmals eine Geschichte erzählt, die eine anschauliche Vorstellung ermöglichen soll oder die zeigen soll, wieso das beschriebene Spiel wichtig ist. Zum Beispiel ist die Geschichte der beiden Gefangenen im Gefangenendilemma die Cover story zu dem Spieltyp der sozialen Dilemmata.
Der Begriff Cover story ist oft etwas abwertend oder lustig gemeint, weil die Geschichten meist nicht exakt die Entscheidungssituation des Spiels wiedergibt, sondern zahlreiche „Verunreinigungen“ durch Assoziationen enthält, die im reinen Spiel nicht vorhanden sind. Man muss deshalb sehr gut aufpassen, ob ein Spiel analysieren will (dann sieht man am besten nur auf die abstrakten Regeln) oder ob man das Spiel als Modellierung einer Situation der echten Welt betrachtet. In diesem Spiel sollte die Interpretation mehr sein als nur eine Cover story.
Diskoordinationsspiel
Der Begriff des Diskoordinationsspiels hat besonders bei Zweipersonenspielen eine sinnvolle Bedeutung. Ein Diskoordinationsspiel ist ein Spiel, bei dem einer der Spieler versucht, „das gleiche“ wie der andere zu tun, wogegen der andere versucht, „etwas anderes“ zu tun.
Ein typisches Beispiel ist das Inspektoren-Spiel, bei dem ein Inspektor eine andere Person fangen will; die flüchtige Person versucht, dem Inspektor auszuweichen, wogegen der Inspektor versucht, sie zu treffen. Das führt dann zu einem Spiel ohne Nash-Gleichgewicht in reinen Strategien.
Dies ist auch die allgemeine Definition des Diskoordinationsspiels: Diskoordinationsspiele sind Spiele ohne Nash-Gleichgewicht in reinen Strategien (->Strategie).
Dominante Strategie
Dieser Begriff kann zweierlei bedeuten: 1. Die Strategie, die eine andere Strategie desselben Spielers im paarweisen Vergleich dominiert. 2. Eine Strategie, die alle anderen Strategien derselben Spielerin dominieren. Mehr dazu in dem Beitrag über die dominante Strategie und unter -> dominierte Strategie.
Dominierte Strategie
Eine Strategie A dominiert eine Strategie B, wenn A nie schlechter, aber mindestens einmal besser ist als B. Besser/schlechter heißt: höhere/niedrigere Auszahlung; „nie“ heißt: bei keinem möglichen Verhalten der Gegenspieler oder der Natur. Genaueres finden Sie in dem Beitrag über die dominante Strategie.
Man muss beachten, dass sich die Definition der Dominanzbeziehung auf Paare von Strategien eines Spielers beziehen. Paare heißt: Die Dominanz lässt sich nur zwischen zwei Strategien eines Spielers feststellen, nicht für ganze Gruppen von Strategien. Eines Spielers heißt: Man darf nicht die Auszahlungen der verschiedenen Spieler mischen.
Dynamische Interpretation des Nash-Gleichgewichts
Wann immer das Wort dynamisch auftaucht, ist damit „im Zeitablauf“ gemeint.
Bei der dynamischen Interpretation des -> Nash-Gleichgewichts wird so getan, als unterlägen die Spieler einem Lernprozess (oder einem andersartigen Entwicklungsprozess), durch den sie das Nash-Gleichgewicht finden. Meistens ist in dieser Interpretation stillschweigend die Annahme versteckt, dass die Spieler nur eingeschränkt rational sind, weil sie bei vollständiger Rationalität direkt zum Nash-Gleichgewicht springen würden (dies wäre dann die statische Interpretation des Nash-Gleichgewichts).
-> Nash selbst hatte wohl eher die statische Interpretation im Kopf, wogegen der (über hundert Jahre ältere) Vorläufer -> Cournot noch eine dynamische Variante beschreibt.
Dynamisches Spiel
Wann immer das Wort dynamisch auftaucht, ist damit „im Zeitablauf“ gemeint.
Ein dynamisches Spiel bezeichnet daher ein Spiel, in dem die Zugreihenfolge tatsächlich als Zeitablauf interpretiert werden kann oder ein Spiel, in dem die Zeit eine Rolle spielt.
Einmal-Spiel
Ein Spiel, das genau einmal gespielt wird und bei dem die Spieler keinerlei gemeinsame Vergangenheit oder Zukunft haben. Sehr oft beziehen sich spieltheoretische Analysen auf Einmalspiele, ohne dass es ausdrücklich dazu gesagt wird.
Die Annahme, dass sich die Spieler in der Zukunft nicht wiederbegegnen werden, ist wichtig, weil sie andernfalls ein anderes Spiel spielen als das, was man gerade analysieren will. Denn wenn in dem analysierten Spiel einer der Spieler Opfer einer unangenehmen Handlung wird, dann könnte er sich eventuell versuchen, in der Zukunft zu rächen – und diese Möglichkeit müsste mit in die Analyse aufgenommen werden.
Siehe auch -> wiederholte Spiele.
Einpersonenspiel
(Unechtes) Spiel, an dem nur ein vernunftbegabter Spieler teilnimmt. Der „Gegenspieler“ ist in der Regel eine Wahrscheinlichkeitsverteilung, mit anderen Worten, der Spieler nimmt an einer -> Lotterie teil. Es handelt sich somit um die Darstellung der Situation der -> klassischen Entscheidungstheorie in der Sprache der Spieltheorie, deren Lösungen durch die Theorie der Glückspiele beschrieben sind.
Ich habe die Einpersonenspiele als unecht bezeichnet, weil die Besonderheiten der Spieltheorie aus dem Wechselspiel mehrerer vernunftbegabter Spieler entsteht, die hier nicht gegeben ist. Formal handelt sich allerdings um ein wohldefiniertes, wennauch weitgehend triviales Spiel.
Entscheidungstheorie
Siehe -> klassische Entscheidungstheorie.
Einige Autoren bezeichnen die Spieltheorie als Teilgebiet der Entscheidungstheorie, andere sehen es genau andersherum. Inhaltlich betrachtet ist sicherlich die erste Interpretation zutreffend (wobei dann Entscheidungstheorie als allgemeine Bezeichnung verwendet wird, nicht im Sinne der klassischen Entscheidungstheorie), mathematisch die zweite, weil sich alle Probleme der klassischen Entscheidungstheorie als (triviale) Spiele im Sinne der Spieltheorie darstellen lassen.
Gefangenendilemma
Grundtyp der sozialen Dilemmata, bei denen aus individueller Sicht ein kooperatives Verhalten nicht gewählt werden kann, weil dieses Verhalten eine -> dominierte Strategie ist.
Hier ist mehr zum Gefangenendilemma.
Gemischte Strategie
Wählt ein Spieler eine gemischte Strategie, dann wählt er keine seiner reinen Strategien direkt aus, sondern er wählt statt dessen einen Zufallsmechanismus aus, der anschließend eine reine Strategie wählt. Formal ist eine gemischte Strategie also eine Wahrscheinlichkeitsverteilung über die reinen Strategien eines Spielers, bei der mindestens zwei Strategien mit positiver Wahrscheinlichkeit ausgewählt werden.
Wenn ein Spieler über alle seine reinen Strategien mischt (er also jede mit positiver Wahrscheinlichkeit wählt), dann nennt man dies einevollständig gemischte Strategie.
Wenn Sie mehr wissen möchten: hier ein ausführlicherer Beitrag zur gemischten Strategie.
Gleichgewicht
In der Spieltheorie wird unter Gleichgewicht meist automatisch das -> Nash-Gleichgewicht verstanden.
inferiore Strategie
Eine Strategie heißt inferior, wenn sie nie als einzige -> beste Antwort ist und es mindestens einen Fall gibt, in dem sie nicht beste Antwort ist. Man kann das Konzept der inferioren Strategie als Verallgemeinerung der -> dominierten Strategie auffassen: Auch bei der inferioren Strategie kann man sich immer besser stellen, wenn man eine andere (nicht inferiore) Strategie wählt; nur dass hier die Überlegenheit nicht durch eine einzelne anderen Strategie besteht, sondern durch einer Kombination aus anderen Strategien (nämlich immer derjenigen, die im konkreten Fall beste Antwort ist).
Initialer Zufallszug
Dies ist ein Zufallszug zu Beginn eines Spiels, der bei Spielen mit unvollständiger Information auswählt, welches Spiel eigentlich gespielt wird.
Klassische Entscheidungstheorie
Die klassische Entscheidungstheorie untersucht Situationen, in denen ein vernunftbegabter Entscheider (= Spieler) gegen eine Wahrscheinlichkeitsverteilung spielt (also gegen die -> „Natur“).
Formal gesehen ist die Situation der klassischen Entscheidungstheorie die eines Einpersonenspiels, das durch die Theorie der Glückspiele beschrieben wird. Sie unterscheidet sich dramatisch von der Spieltheorie (die aus der Theorie der Gesellschaftsspiele hervorgegangen ist), weil die Natur nicht auf den persönlichen Spieler reagiert oder dessen potenzielle Handlungen in das eigene Verhalten einfließen lässt.
Kooperative Spiele, kooperative Spieltheorie
-> nichtkooperative Spiele.
Konstantsummenspiel
-> Nullsummenspiel.
Lotterie
Eine Lotterie ist ein Spiel, das nur aus einem einzigen Zufallszug besteht, bei dem der Spieler also nichts selber entscheiden kann.
Sehr häufig werden elementare Lotterien verwendet, die nur zwei Ergebnisse haben können. Nennen wir diese beiden Ergebnisse dieAuszahlung a und die Auszahlung b. Dann wird die Lotterie oft geschrieben als L = (a; p; b; 1-p), was soviel heißt wie: In der Lotterie L kann man entweder a gewinnen oder b, und zwar gewinnt man a mit einer Wahrscheinlichkeit von p und b mit einer Wahrscheinlichkeit von 1-p. Als Baum sieht das dann folgendermaßen aus:
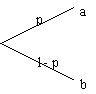
Ein Anwendungsbeispiel findet sich in dem Beitrag über das Wahlrecht.
Mechanismusdesign, Mechanismus-Design, Mechanismus-Design-Theorie
Mechanismusdesign bezeichnet den Vorgang, die spieltheoretische Analyse rückwärts anzuwenden: Statt zu fragen, wie die Spieler ein gegebenes Spiel spielen werden, fragt man, wie man ein Spiel gestalten (designen) muss, damit es auf eine bestimmte Weise gespielt wird. Die gestalteten Regeln des Spiels heißen dann Mechanismus.
Ein bekanntes Anwendungsgebiet ist die Gestaltung von Marktregeln, also dem Marktmechanismus. Während in der klassischen volkswirtschaftlichen Analyse von dem genauen Marktmechanismus abstrahiert wird, spielen die Detailregeln in der realen Welt eine entscheidende Rolle. Das Mechanismusdesign fragt hier, wie man die marktlichen Regeln gestalten sollte, um bestimmte Ziele zu erreichen. Die Gestaltung wird dann von einer übergeordneten Instanz übernommen, in volkswirtschaftlichen Zusammenhängen oft vom Gesetzgeber.
Für die Mechanismus-Design-Theorie sind die drei Forscher Leonid Hurwicz, Eric Maskin und Roger Myerson im Jahr 2007 mit dem Wirtschafts-Nobelpreis ausgezeichnet worden.
Ich habe noch einen längeren Beitrag zur Mechanismus-Design-Theorie. Auch das von mir herausgegebene Buch Coopetition beschäftigt sich damit, wie man die Regeln seiner Geschäftsbeziehungen gestaltet und ist damit eine anwendungsbezogene Anleitung zum Mechanismusdesign im Geschäftsleben.
Mengenoligopol, Mengenwettbewerb
-> Cournot-Oligopol, Cournot-Wettbewerb.
Modellierung, modellieren
Modellierung ist der Vorgang, eine reale Situation mit spieltheoretischen Mitteln darzustellen. Ursprünglich bezog sich dieser Begriff auf das Aufstellen eines mathematischen Modells (hiervon ist der Begriff „Modellieren“ abgeleitet), aber die im Deutschen vorhandene ursprüngliche Bedeutung des Wortes ist durchaus zutreffend, weil es prinzipiell beliebig viele verschiedene Möglichkeiten der Modellierung eines Sachverhalts gibt. Daher ist das Modellieren durchaus als ein kreativer und subjektiver Prozess zu sehen.
Mehr zur Modellierung in dem Einführungsbeitrag über Spieltheorie.
Monopol
In einem (Angebots-) Monopol steht ein Anbieter vielen Nachfragern gegenüber. Diese Situation wird meistens so modelliert (also spieltheoretisch dargestellt), dass nur der Monopolist vernunftbegabt handelt, wogegen die vielen Nachfrager für sich allein genommen zu klein sind als dass sie einen Einfluss auf das Ergebnis haben könnten. (Gleichzeitig muss auch gelten, dass sich die Nachfrager nicht koordinieren können.) Die Situation wird dann zu einem Einpersonenspiel, das beim Übergang zum Oligopol zu einem Mehrpersonenspiel wird.
Die wohl älteste spieltheoretische Analyse beginnt bereits mit dem Monopol und dem Übergang zum Oligopol (Augustin Cournot 1838: Recherches sur les principes mathématiques de la théorie des richesses).
Es gibt zwei Ursachen für ein Monopol: rechtliche Bedingungen und das natürliche Monopol, bei dem das Monopol von allein entsteht, weil – um es salopp auszudrücken – auf dem Markt nur Platz für einen Anbieter ist.
myopische Prozesse, myopische Spieler
Ein Begriff aus der evolutionären Spieltheorie. Myopisch heißt kurzsichtig und beschreibt ein Verhalten, bei dem der betreffende Spieler nur einen (oder wenige) Denkschritte vornimmt anstatt die gesamte Situation bis zum Ende zu durchdenken, wie es ein vollständig rationaler Spieler tun würde.
Ein Beispiel für einen mypischen Prozess ist die Interpretation des -> Cournot-Oligopols, bei der alle Spieler jeweils den aktuellen Preis ihres Konkurrenten als gegeben ansehen und in der nächsten Periode einen Preis setzen, der gegen den derzeitigen Preis des Konkurrenten optimiert. Anschließend sind sie jeweils überrascht, dass ihre Annahme gar nicht gestimmt hat und der Konkurrent zwischenzeitlich auch seinen Preis geändert hat, weil er sich ja die gleichen Überlegungen machen kann. Aber auch aus dieser Beobachtung lernen die beiden nicht, sondern handeln in der nächsten Runde wieder myopisch.
Nash-Gleichgewicht
Ein Nash-Gleichgewicht in eine Strategienkombination, bei der kein Spieler einen Anreiz hat, als einziger von diesem Gleichgewicht abzuweichen. Es ist das zentrale Lösungskonzept der nichtkooperativen Spieltheorie und eine der wichtigsten Entwicklungen in den Sozialwissenschaften des 20. Jahrhunderts. Hier ist eine ausführlichere Darstellung des Nash-Gleichgewichts.
Nash, John Forbes jr.
Erfinder des Nash-Gleichgewichts und dargestellte Person des Films „A Beautiful Mind“. Er erhielt 1994 (zusammen mit Harsanyi und Selten) den Nobelpreis für Wirtschaftswissenschaften. Neben dem Nash-Gleichgewicht prägte er die Unterscheidung in kooperative und nichtkooperative Spieltheorie und definierte weiterhin die Nash-Verhandlungslösung für kooperative Spiele. Historisch betrachtet legten seine Arbeiten den Grundstein dafür, dass die Spieltheorie den Bereich der Mathematik verließ und auf realwissenschaftliche Sachverhalte angewandt werden konnte.
Mehr über John Nash hier.
Natur
Die Natur (manchmal auch „Umwelt“) ist in der klassischen Entscheidungstheorie meist eine Metapher für einen Zufallsspieler, gegen den man in einem Einpersonenspiel spielt. Ein wenig technischer formuliert, ist das eine Wahrscheinlichkeitsverteilung über die verschiedenen Umweltzustände, die die Konsequenzen des eigenen Handelns beeinflussen.
Beispiel: Sie spielen Roulette. Ihre Entscheidung besteht darin, eine Zahl zwischen 0 und 36 zu wählen, die Konsequenz dieses Handelns wird durch den Zufallsspieler Rouletterad bestimmt (nämlich entweder verlieren Sie Ihren Einsatz oder Sie versechsundreißigfachen ihn). Die Zahl, auf die die Roulettekugel rollt, ist der Umweltzustand.
Die Besonderheit der Natur besteht darin, dass sie nicht vernunftbegabt ist, keine eigenen Interessen verfolgt und daher unabhängig von den persönlichen Spielern „entscheidet“.
Natürliches Monopol
Ein natürliches Monopol liegt vor, wenn – einfach gesagt – nur Platz für einen Anbieter ist. Dann entsteht das Monopol von allein und ist stabil, obwohl auch mehrere Anbieter nebeneinander existieren dürften. (Dies unterscheidet es von rechtlichen Monopolen: dort wird politisch per Gesetz bestimmt, dass nur ein Anbieter existieren darf, oft ist das dann ein Staatsmonopol. Dies war zum Beispiel lange Zeit bei der Post der Fall.)
Es gibt zwei wesentliche Ursachen für ein natürliches Monopol: 1. Betriebsgrößenersparnis, durch die die Produktion pro Stück mit zunehmender Unternehmensgröße sehr viel billiger wird. 2. Netzwerkeffekte, durch die sich die Marktteilnehmer auf einen Anbieter koordinieren und dadurch keinen individuellen Anreiz mehr haben, von dem erreichten Zustand abzuweichen. Das passiert zum Beispiel oft im Technologiebereich, in dem die Marktteilnehmer es bevorzugen, denselben Standard zu verwenden wie andere, z.B. um Daten auszutauschen.
Nichtkooperative Spieltheorie, nichtkooperative Spiele
Teilgebiet der Spieltheorie, das nur Spiele untersucht, in denen die Spieler keine bindenden Verträge schließen können.
Die Unterscheidung in „kooperative“ und „nichtkooperative“ Spiele geht auf John F. Nash zurück, wird aber oft missverstanden. Die Unterteilung besagt nicht, dass in nichtkooperativen Spielen keine Kooperation möglich sei. Der Unterschied besteht lediglich darin, dass bei kooperativen Spielen die Kooperation als gegeben vorausgesetzt wird, wogegen in nichtkooperativen Spielen erklärt werden muss, wie sie entsteht.
Intuitiv kann man sich die Situation der nichtkooperativen Spiele so vorstellen: Die Spieler sitzen vor dem Spiel zusammen und sprechen miteinander, aber dann trennen sie sich und entscheiden über ihre Züge völlig unabhängig von den anderen Spielern. Folglich können sie zwar versprechen oder drohen, einen bestimmten Zug zu tun, aber was sie dann wirklich tun, kann davon abweichen. Sofern in dem Spiel Kooperation möglich ist, so können die Spieler also durchaus auch in der nichtkooperativen Spieltheorie kooperieren, aber das steht nicht von vornherein fest, sondern ergibt sich als Entscheidung im Spiel.
In einer extremen Auffassung (die heute vorherrscht) gibt es noch nicht einmal die Kommunikation vor dem Spiel.
Normalform
Die Normalform ist eine Darstellungsform für Spiele, also eine Art und Weise, wie man ein Spiel aufschreiben kann. Bei der Normalform werden alle Strategien aller Spieler einander gegenübergestellt, sodass man in einer Art Tabelle die Spielausgänge für alle Strategienkombinationen ablesen kann. Bei zwei Spielern entsteht tatsächlich eine zweidimensionale Tabelle, bei drei Spielern würde ein dreidimensionale Tabelle entstehen, bei noch mehr Spielern wird es unanschaulich, denn man müsste man eine multidimensionale Tabelle zeigen. Es entstehen also Objekte, die man nur noch mathematisch beschreiben kann.
Dennoch ist für den Zwei-Personen-Fall die Normalform sehr anschaulich. Ein Beispiel für ein Zweipersonenspiel mit je drei Strategien für jeden Spieler ist das folgende Spiel:
|
Engagement auf dem Markt: |
Spielerin 2: |
|||
|
a (gering) |
b (mittel) |
c (stark) |
||
|
1 (gering) |
(18,18) |
(15,19) |
(10,21) |
|
|
Spieler 1: |
2 (mittel) |
(19,15) |
(16,16) |
(11,15) |
|
3 (stark) |
(21,10) |
(15,11) |
(9,9) |
|
Die beiden Spieler haben hier die drei Strategien „gering“, „mittel“ und „stark“. Die Kombination der beiden Einzelentscheidungen führt zu einem Tabelleneintrag, der einem Spielausgang entspricht. Die beiden Zahlen dort sagen, wieviel jeder Spieler bei diesem Spielausgang als -> Auszahlung bekommt.
Nullsummenspiel
Nullsummenspiele haben besonders dann eine Bedeutung, wenn es sich um Zweipersonenspiele handelt. Bei einem Zweipersonen-Nullsummenspiel verliert der eine Spieler das, was die andere Spielerin gewinnt. Die Interessen sind in diesen Spielen völlig entgegengesetzt, die Spieler haben keinerlei gleichgerichtete Interessen.
Der Name Nullsummenspiel stammt daher, dass in diesen Spielen die Auszahlungssumme über beide Spieler immer genau null beträgt (weil der Gewinn des einen ja der Verlust des anderen ist). Es ist allerdings nicht wichtig, dass sich die Auszahlungssumme immer zu genau null addiert, jeder andere konstante Wert würde zu strategisch äquivalenten Spielen führen. Spiele, deren konstante Auszahlungssumme über alle Spieler ungleich null ist, heißen Konstantsummenspiele.
Man kann die Definition des Nullsummenspiels natürlich auch auf Mehrpersonenspiele übertragen, aber dort ist die Nullsummeneigenschaft von geringerer Bedeutung.
Wenn Sie einmal einen interessanten Roman lesen möchten, der beschreibt, was passiert, wenn die Spieler eine Situation als Nullsummenspiel wahrnehmen, dann lesen Sie Fiasko von Stanislaw Lem (aber Vorsicht: der Titel ist Programm).
Nutzen
In der Spieltheorie ist der Begriff des Nutzens oft synonym zu dem der -> Auszahlung. Es handelt sich um ein Maß für die „Freude“, die eine Person aus einem bestimmen Spielausgang zieht. So einfach dieser Ausgangspunkt ist, so kompliziert ist die mathematische Nutzentheorie geworden.
Verkompliziert wird eine Behandlung des Nutzens, weil vielfach die zu bewertenden Ereignisse nicht mit Sicherheit eintreten, sondern risikobehaftet sind, es sich also um -> Lotterien handelt. Hieraus ist dann der Begriff des Risikonutzens entstanden.
o. B. d. A.
Abkürzung für „ohne Beschränkung der Allgemeingültigkeit“ oder „ohne Beschränkung der Allgemeinheit“. Eine in der Mathematik häufig benutzte Abkürzung, mit der man darauf hinweist, dass eine scheinbar einschränkende Annahme die Allgemeingültigkeit der Analyse nicht aufhebt.
Oligopol
In einem (Angebots-) Oligopol stehen mehrere Anbieter vielen Nachfragern gegenüber. Indem man die Nachfrager als zu klein ansieht, als dass sie das Ergebnis beeinflussen könnten, stehen die wenigen Anbieter in einem Wettbewerb zueinander, in dem jeder vernunftbegabt ist und einen wesentlichen Einfluss auf das Ergebnis hat. Es handelt sich somit um den klassischen Fall der spieltheoretischen Interaktion, der bereits 1838 von Augustin Cournot behandelt wurde. Mehr dazu unter -> Monopol.
Pareto-Effizienz, Pareto-Optimalität
Eine Aufteilung ist Pareto-effizient, wenn man keinen Beteiligten besser stellen kann, ohne einen anderen schlechter zu stellen.
Sehr oft wird von „Pareto-optimal“ gesprochen, aber dieser Begriff ist irreführend, denn der Zustand braucht überhaupt nicht „optimal“ zu sein; vielmehr ist dies die klassische Definition für Effizienz, daher wird in der Spieltheorie meist der Begriff „Pareto-effizient“ verwendet.
Partie
Eine Partie ist eine Abfolge von Zügen vom Spielbeginn bis zu einem Ausgang des Spiels. Sie endet mit Auszahlungen an jeden der beteiligten Spieler. In einer Partie können auch Zufallszüge vorkommen.
Man darf eine Partie nicht mit einer Strategie verwechseln: Bei der Partie kommt es nur darauf an, dass am Ende ein Spielausgang erreicht wird. Eine Strategie muss dagegen exakt angeben, was in jedem möglichen Fall zu tun ist, sie muss also auch Anweisungen dazu geben, was abseits einer gegebenen Partie geschehen soll.
Preisoligopol, Preiswettbewerb
-> Bertrand-Wettbewerb
Principal
Siehe Principal-Agent-Theorie.
Principal-Agent-Theorie
Die Principal-Agent-Theorie befasst sich mit Situationen, in denen eine Person eine andere beauftragt, etwas zu tun. Klassisches Beispiel ist die Unternehmensinhaber-Manager-Beziehung. In dieser Beziehung ist der ausführende Manager der Agent, der beauftragende Inhaber ist der Principal. Die spieltheoretische Komponente besteht darin, dass der Principal dem Agent nicht alles exakt vorschreiben kann (sonst könnte er es ja selber machen) und/oder nicht beobachten kann, was der Agent tatsächlich tut. Dadurch entsteht ein Konflikt zwischen diesen beiden Spielern.
Prospect Theory
Eine deskriptive Entscheidungstheorie, die das Verhalten von Menschen in bezug auf Risiko beschreibt. Kurz gesagt behauptet diese Theorie, dass sich Menschen normalerweise risikoavers verhalten, aber auf Risikofreude umschalten, wenn sie eine Situation als Verlust wahrnehmen.
Der im Deutschen etwas eigentümlich klingende Name der Theorie stammt von dem englischen Wort prospect, das hier so viel wie „Gewinnaussicht“ heißt. Die Theorie wurde aufgrund von Untersuchungen entwickelt, in denen Probanden befragt wurden, wie gern sie verschiedene -> Lotterien mögen. Die Autoren der Untersuchung verwendeten dabei nicht das Wort lottery, sondern eben prospect.
Die Theorie stammt von David Kahneman und Amos Tversky aus dem Jahr 1979. Kahneman wurde dafür 2002 der Nobelpreis in Wirtschaftswissenschaften verliehen. Mehr zur Prospect Theory hier.
Purification gemischter Strategien
Die gemischte Strategie ist ein mathematisches Konzept, das für viele Entscheidungen in der realen Welt wenig Überzeugungskraft besitzt. Daher wird oft der Versuch unternommen, Interpretationen zu liefern, die über die reine Zufallsauswahl einer reinen Strategie hinausgehen.
Derartige Interpretationen sind: Man spielt gar nicht gegen einen einzelnen Spieler, sondern gegen eine Population von Spielern, von denen jeder einzelne eine reine Strategie spielt. Da aber der Gegenspieler zufällig aus der Population gewählt wird, ist die Wirkung so wie wenn dieser zufällig mischen würde.
Oder: Das gespielte Spiel ist ein Spiel mit unvollständiger Information, in dem es mehrere Typen des Gegenspielers gibt. Dieser Typ wird durch einen initialen Zufallszug ausgewählt, was im Ergebnis so wirkt, wie wenn der Gegenspieler mischt (obwohl jeder Typ eine reine Strategie spielt).
Reine Strategie
-> Strategie (reine Strategie), -> gemischte Strategie
Risiko
Risiko ist ein schwer zu fassender Begriff, aber als Risiko wird heutzutage üblicherweise eine Situation bezeichnet, in der es unterschiedliche Ergebnisse geben kann, die die Entscheider unterschiedlich stark mögen (kurz gesagt, eine Situation, in der unterschiedliche -> Auszahlungen möglich sind). Die Tatsache, dass es unterschiedliche Auszahlungen gibt, kann man auch so beschreiben, dass man zwar eine Auszahlung erwartet, dass es aber Abweichungen von dieser Erwartung geben kann. Als Erwartung bezeichnet man hier meist den mathematischen Erwartungswert der Auszahlungen, der durch die Auszahlungen selbst und durch deren Eintrittswahrscheinlichkeiten bestimmt wird. Daher kommt die oftmals verwendete Definition, „Risiko ist die Möglichkeit einer Abweichung vom Erwarteten“.
Einige Autoren, besonders aus der klassischen Entscheidungstheorie, unterscheiden zwischen „Risiko im engen Sinn“ und „Unsicherheit“. Beim Risiko im engen Sinn sind die Wahrscheinlichkeiten der verschiedenen Ergebnisse bekannt, bei Unsicherheit noch nicht einmal diese.
Implizit meint man mit Risiko meist das Ergebnis eines Zufallsereignisses (-> Zufallszug), nicht das Ergebnis der Handlung eines anderen Entscheiders. Das liegt zum Teil daran, dass man bei Zufallsereignissen an Lotterien denkt, deren Auszahlungen tatsächlich Geldauszahlungen sind, wogegen man bei Mehrpersonenspielen die Auszahlungen bereits als Nutzenwerte interpretiert, bei denen die Entscheider -> risikoneutral sind.
Risikoneutralität, risikoneutral
Eine Person ist risikoneutral, wenn sie bei unsicheren Ergebnissen nur auf den Erwartungswert der Auszahlung achtet und nicht darauf, wie sehr die Ergebnisse von diesem Erwartungswert abweichen können.
Beispiel: Der Person werden zwei mögliche Geschenke angeboten: 100 EUR bar auf die Hand oder eine -> „Lotterie“, bei der eine Münze geworfen wird und bei Kopf 200 EUR geschenkt werden, bei Zahl aber nichts. Der -> Erwartungswert beider Lotterien ist gleich groß, nämlich 100 EUR. Aber bei der zweiten Lotterie gibt es entweder mehr oder weniger als den Erwartungswert, sie ist also mit -> Risiko verbunden. Wenn die Person sich überhaupt nicht für diesen Unterschied interessiert, dann verhält sie sich risikoneutral.
Soziales Dilemma
-> Gefangenendilemma.
Spiel
Als Spiel bezeichnet man eine Entscheidungssituation, die an die Gesellschaftsspiele angelehnt ist: Mehrere Spieler verfolgen individuelle Ziele und treffen Entscheidungen, um ihre Ziele zu erreichen. Die Entscheidungen dürfen nur im Rahmen der Spielregeln erfolgen, und ihre Konsequenzen hängen auch davon ab, was die anderen Spieler tun.
Hier ist mehr zum Spiel.
Spieler
Derjenige, der im Spiel Entscheidungen nach anderen Kriterien trifft als der Zufall. Sehr oft wird von vernunftbegabten Spielern ausgegangen, es gibt aber auch wichtige Bereiche der Spieltheorie, die sich mit dem Verhalten von Tieren, Pflanzen oder auch Molekülen beschäftigen.
Interessanterweise ist es oft nicht so einfach festzulegen, was eigentlich ein Spieler ist. Was ist zum Beispiel bei Gruppen von Personen? Kann man ein Unternehmen als einen Spieler modellieren oder liegen hier bereits so offensichtliche Interessenkonflikte vor (zum Beispiel zwischen Chef und Ausführendem), sodass man die Einheit „Unternehmen“ in mehrere Entscheider aufspalten muss? Und wenn ja, in welche? Dies ist die Hypothese, der die Principal-Agent-Theorie zugrunde liegt, wogegen lange Zeit in der klassischen Mikroökonomie vom Unternehmen als einer elementaren Entscheidungseinheit ausgegangen wurde.
Aber selbst eine reale Person muss noch lange nicht die kleinste Entscheidungseinheit sein und damit auch nicht ein Spieler im Sinne der Spieltheorie: Was passiert zum Beispiel, wenn heute eine Person eine Drohung ausspricht, die sie problemlos ausführen könnte, deren Ausführung aber sehr teuer wäre? Kann sie sich tatsächlich heute schon selbst darauf festlegen es zu tun, oder spielt sie gewissermaßen gegen ihr eigenes Ich in der Zukunft, zerfällt also in mehrere Spieler (die man hier -> Agenten desselben Spielers nennt)? Diese Ansicht vertritt zum Beispiel Reinhard Selten mit seinem Konzept der Agentennormalform.
Hier ein Anwendungsbeispiel, bei dem ein Spieler in seine Agenten zerfällt.
Spieltheorie
Die Theorie, die sich mit den Entscheidungen in Situationen beschäftigt, in denen das Ergebnis nicht durch einen Entscheider allein hervorgebracht wird, sondern durch das Zusammenwirken von mehreren Entscheidern.
Die Spieltheorie wurde ursprünglich wegen ihrer Methodik als Teilgebiet der (angewandten) Mathematik angesehen, wurde dann aber besonders in den Wirtschaftswissenschaften auf die verschiedensten Gebiete angewandt und hat sich damit zu einer Sozialwissenschaftentwickelt, die methodisch vom Individuum ausgeht. Daneben wird sie auch erfolgreich in den Naturwissenschaften angewandt, zum Beispiel in der Biologie (sehr oft im Zusammenhang mit der Evolutionstheorie).
Hier ist eine längere Einführung in die Spieltheorie.
Statische Interpretation des Nash-Gleichgewichts
Statisch deutet immer auf einen Sachverhalt hin, der ohne Berücksichtigung der Zeit dargestellt wird.
Bei der statischen Interpretation des -> Nash-Gleichgewichts wird so getan, als handelten alle Spieler nach den gleichen Rationalitätsgrundsätzen, die sie unabhängig voneinander das Nash-Gleichgewicht als Lösung des Spieles erkennen lassen. Daher springen sie ohne weitere Zwischenschritte direkt zum Nash-Gleichgewicht.
Problematisch an dieser Interpretation ist, dass die Spieler dieselbe Rationalität zugrunde legen müssen und dass nicht klar ist, zu welchem Nash-Gleichgewicht sie springen, wenn es mehrere „gleich gute“ Nash-Gleichgewichte gibt.
Der Gegensatz zur statischen Interpretation ist die -> dynamische Interpretation des Nash-Gleichgewichts.
Strategie (reine Strategie)
Eine Strategie ist ein vollständiger Verhaltensplan eines Spielers. Eine Strategie im spieltheoretischen Sinn muss mehr angeben als eine Strategie im Alltagssinn, nämlich eine exakte Handlungsvorschrift („Zug„) für jede Situation, in die der Spieler kommen kann.
Oftmals wird allerdings ein derartiger Verhaltensplan in der spieltheoretischen Darstellung einfach auf den Namen der Strategie reduziert. Es sieht dann so aus, als könne der betreffende Spieler einfach nur zwischen wenigen, einfachen Alternativen wählen, also zum Beispiel zwischen den Strategien A und B. Man sieht dann nicht mehr, dass sich hinter den harmlosen Namen eigentlich komplexe Verhaltenspläne verbergen, sondern es sieht so aus, als hätte das gesamte Spiel nur einen einzigen Zug. Es ist wichtig, die Strategie nicht mit einer Partie zu verwechseln.
Wenn man deutlich machen möchte, dass eine Spielerin eine Strategie direkt (ohne zwischengeschalteten Zufallsmechanismus) wählt, dann spricht von einer reinen Strategie (im Gegensatz zu einer gemischten Strategie).
Spielzug
Siehe Zug.
Superspiel
Meist bezeichnet man mit Superspiel ein unendlich oft -> wiederholtes Spiel. Einige Autoren bezeichnen jedes wiederholte Spiel als Superspiel, also auch die endlich wiederholten.
Die möglichen Strategien der Spieler (also die Strategienräume) sind in einem Superspiel wesentlich größer als in dem zugrundeliegenden -> Einmalspiel.
Teilspielperfektheit, teilspielperfektes Nash-Gleichgewicht
Das teilspielperfekte -> Nash-Gleichgeweicht ist eine Verfeinerung des Nash-Gleichgwichts: Teilspielperfektheit fordert, dass die Nash-Gleichgewichtsbedingung nicht nur für das gesamte Spiel gilt, sondern auch für jedes seiner Teilspiele. Ein Teilspiel ist dabei ein Teil des Spiels, den man für sich allein genommen auch als ganzes Spiel ansehen kann. In der Praxis bedeutet Teilspielperfektheit, dass man das Spiel von hinten her löst: Man fragt sich, wie sich der Spieler des letzten Zuges im Spiel entscheidet; mit diesem Wissen fragt man sich nach dem optimalen Verhalten des vorletzten Spielers usw. bis zum Spielanfang.
Das teilspielperfekte Gleichgewicht stammt von Reinhard Selten, der (unter anderem) dafür den Nobelpreis in Wirtschaftswissenschaften erhalten hat. Er hat es in seinem Aufsatz über das „Chainstore-Paradox“ formuliert.
Die Teilspielperfektheit ist eine der wichtigsten Verfeinerungen des Nash-Gleichgewichts überhaupt und wird vielfach einfach stillschweigend angewandt, selbst dann, wenn es noch weitere nicht teilspielperfekte Gleichgewichte gibt. Es ist aber nicht ganz so harmlos wie es auf den ersten Blick scheint. Wen es interessiert, der kann es sehr ausführlich in meinem Spieltheorie-Buch nachlesen.
Typ eines Spielers
Normalerweise sind die Regeln eines Spiels Common knowledge (gemeinsames Wissen). Wenn ein Spieler aber nicht genau weiß, gegen wen er spielt (oder was seine Gegnerin kann oder will), dann sind die Regeln nicht Common knowledge, und das Spiel wäre nicht wohldefiniert. Heutzutage wird diese Situation beseitigt, indem jeder der Spielerinnen, die solche unbekannten Elemente enthalten, Typenzugeordnet werden, die sie sein können. Je nach Typ wird dann ein anderes Spiel gespielt. Diese Spiele werden durch einen Zufallszug am Beginn des Spiels (initialer Zufallszug) ausgewählt.
Sofern man sich nicht über die Wahrscheinlichkeitsverteilung dieses Zufallszugs streiten kann, ist danach das Spiel wieder wohldefiniert.
Der Typ eines Spielers darf nicht mit den -> Agenten eines Spielers verwechselt werden.
Umwelt
Siehe -> Natur.
Umweltzustand
In der klassischen Entscheidungstheorie ist dies ein von der Natur ausgewählter Zustand, der einen Einfluss darauf hat, welche Konsequenzen Ihre Entscheidungen haben. Für Details siehe -> Natur.
Unsicherheit
In der klassischen Entscheidungstheorie wird als Unsicherheit eine Situation bezeichnet, in der verschiedene Spielausgänge möglich sind, aber keinerlei Informationen über die Wahrscheinlichkeiten vorliegen, mit der die Ereignisse eintreten können. Es ist dann ein Spezialfall des -> Risikos.
In der heutigen Spieltheorie wird überwiegend angenommen, zumindest die Wahrscheinlichkeiten für Zufallsereignisse seien allen Spielern bekannt (noch genauer gesagt: sie seien Common knowledge und daher auch für alle Spieler identisch).
Vollständig gemischte Strategie
-> gemischte Strategie
Wiederholtes Spiel
Wenn ein -> Einmalspiel mehrfach hintereinander gespielt wird, dann nennt man es ein wiederholtes Spiel.
Durch die Wiederholung ergeben sich neue strategische Möglichkeiten gegenüber dem Einmalspiel, weil jetzt jeder Spieler in späteren Wiederholungen seine Entscheidungen vom Verhalten der Gegener aus früheren Wiederholungen abhängig machen kann. Daher sind die Strategien im wiederholten Spiel sehr viel komplexer als im Einmalspiel.
Manche Autoren bezeichnen jedes wiederholte Spiel auch als -> Superspiel, andere nennen nur unendlich oft wiederholte Spiele Superspiele.
Win-Win-Spiel
Ein Win-Win-Spiel ist ein Koordinationsspiel mit einem Nash-Gleichgewicht, das auszahlungsdominant gegenüber allen anderen Nash-Gleichgewichten desselben Spiels ist.
Die Besonderheit besteht darin, dass die Spieler völlig gleichgerichtete Interessen haben, es aber durch die Gleichzeitigkeit des Ziehens dennoch zu Koordinationsversagen kommen kann. Ein Win-Win-Spiel ist ein Extremfall der -> Coopetition und liegt strategisch diametral gegenüber dem Nullsummenspiel.
Zufallszug
Während eines Spiels kann es auch sein, dass Zufallsereignisse eintreten (in Gesellschaftsspielen sind dies zum Beispiel der Wurf eines Würfels). Diese werden in der Spieltheorie formal genauso dargestellt wie wenn ein persönlicher Spieler ziehen würde (also wie ein Zug), zusätzlich werden noch die Wahrscheinlichkeiten angegeben, mit denen der Zufall die verschiedenen Ereignisse auswählt.
Der Fall eines persönlichen Spielers gegen einen Zufallszug ist der Fall der klassischen Entscheidungstheorie.
Der initiale Zufallszug ist formal gesehen ein „normaler“ Zufallszug, aber die Interpretation ist meist eine im Sinne eines Spiels mit unvollständiger Information.
Zug (Spielzug)
Die Entscheidung zu einem bestimmten Zeitpunkt im Spielablauf ist ein Zug. Eine Abfolge von Zügen vom Spielbeginn bis zu einem Spielende ergibt eine Partie. Man darf beides nicht mit einer Strategie verwechseln, obwohl es in der Normalform-Darstellung so aussieht, als bestehe das gesamte Spiel lediglich aus einem Zug pro Spieler.