Version vom 24.05.2006
Erstversion vom April 2006

Wieviel ist ein Wahlrecht wert?

Auf dem Tisch liegen zwei Stücke Kuchen: Ein Stück Frankfurter Kranz (Ihr Lieblingskuchen) und ein Stück staubiger Kokosstreusel (Ihr kuchenmäßiger Gau). Wie schön, dass Sie Gast sind und daher wählen dürfen. – Aber ist es immer schön, wählen zu dürfen? Und wie schön ist es eigentlich?

Und ja: „wählen dürfen“ bezieht sich auch auf Bundestagswahlen und auf finanzielle Derivate namens Optionen (was nur die englische Übersetzung der Wahlmöglichkeit ist). Und so kommen wir in diesem Kapitel vom harmlosen Kuchen essen über Politik und Finanztheorie zur Philosophie.

Wie gern wählen wir?

Um zu entscheiden, wie schön das Wählen ist, müssen wir uns einfach nur vorstellen, wir dürften es nicht. Damit es auch schön fair zugeht, wirft dann in unserem Beispiel von eben unsere Gastgeberin einfach eine Münze, um zu entscheiden, wer welches Stück bekommt.

Werfen wir also einen Blick auf die Situation, in der ein Münzwurf entscheidet, welches Stück Kuchen wir bekommen. In der Spieltheorie nennt man dies einen Zufallszug oder wenn – wie hier – nur dieser eine Zug den Spielausgang bestimmt, dann ist es eine Lotterie. Wir können dies als einen sehr einfachen Spielbaum schreiben:

 

 

 

 

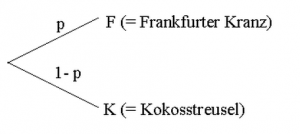
F ist die Freude[1], die wir beim Verzehr des Frankfurter Kranzes haben, K die Freude für den Kokosstreusel. Da wir den Frankfurter Kranz lieber mögen als den Kokosstreusel, ist .

Wir wissen jetzt: Wenn wir wählen dürfen, dann nehmen wir immer das Stück Kuchen, das uns die größere Freude stiftet (hier also den Frankfurter Kranz, der uns eine Freude von F gibt). Wenn gelost wird, dann hängt unsere Freude vom Ergebnis des Losens ab und dieses wiederum hängt von den Wahrscheinlichkeiten ab, mit denen die beiden Lotterieergebnisse eintreten. Wenn eine Münze geworfen wird, dann ist das schöner für uns als wenn wir den Frankfurter Kranz nur dann bekommen, wenn wir mit einem normalen Würfel eine Sechs würfeln.

Folglich müssen wir die Wahrscheinlichkeit für die zufällige Wahl des Frankfurter Kranzes mit einbeziehen und bezeichnen diese einfach als p (für probability). Eine Wahrscheinlichkeit von p = 100% bedeutet, dass wir in der Lotterie immer den Frankfurter Kranz bekomme, eine von p = 50% bedeutet, dass zum Beispiel die Münze geworfen wird. Die Wahrscheinlichkeit für den Kokosstreuselkuchen ist einfach die Wahrscheinlichkeit, dass wir nicht den Frankfurter Kranz bekommen. Da wir mit 100% entweder den einen oder den anderen bekommen, ist also 100% minus p die Wahrscheinlichkeit, die noch für den Kokosstreusel übrig bleibt. Da 100% nur eine andere Schreibweise für 1[2], ist also die Wahrscheinlichkeit für Kokosstreusel in der Lotterie immer gleich 1-p.

Wenn wir wissen möchten, wieviel wir durch das Wahlrecht gewinnen, dann müssen wir von dem Wert, den wir wählen werden (also von F) das abziehen, was wir im anderen Fall bekommen würden. Die zusätzliche Freude durch das Wahlrecht ist also:

W = F – [p F + (1-p) K]

Nach einigen Umformungen[3] wird daraus

W = (1-p) (F-K)

Dieses Ergebnis sagt uns etwas sehr Einfaches – nämlich dass es zwei Einflussgrößen gibt, die unsere Freude über das Wahlrecht erhöhen: 1. Wir wählen umso lieber, je größer die Wahrscheinlichkeit ist, dass wir zufällig den Kokosstreusel bekommen würden, den wir nicht mögen (in der Formel ist das 1-p). 2. Das Wählen wird für uns umso wertvoller, je größer der Unterschied zwischen den beiden Alternativen ist (in der Formel ist das F-K). Ob das Wahlrecht für uns wertvoll oder wertlos ist, hängt demnach nicht davon ab, ob wir die beiden Alternativen überhaupt gut oder schlecht finden, sondern ausschließlich davon, wie sehr sie sich voneinander unterscheiden.

Werden wir praktischer: Wahlrecht in der echten Welt

Wieso sind Bundestagswahlen so frustrierend?

Gut, wir dürfen wählen. Aber zum einen zählt unsere Stimme recht wenig (was ein ganz eigenes Kapitel in der Spieltheorie ist, aber lassen wir das hier einmal beiseite) und zum anderen sind die zu wählenden Alternativen sehr ähnlich. (Zumindest sind die Unterschiede gering genug, dass sogar eine große Koalition kein Problem ist – also, seien wir ehrlich – wie groß können die wahren Differenzen über die Sonntagsreden hinaus schon sein?) Nicht sehr groß, und das lässt die Differenz zwischen den beiden Alternativen (F-K) schrumpfen. Und damit schrumpft der Wert unseres Wahlrechts.

Aber Vorsicht: keine falschen Schlüsse ziehen. Das heißt nicht, dass wir uns bei sehr unterschiedlichen Parteien wohler fühlen würden. Es heißt nur, dass das Recht der Wahlausübung dann mehr wert wäre.

Optionen

Tief im Giftschrank der Finanzinstrumente stehen die Optionen. Das sind Instrumente die einem das Recht, nicht aber die Pflicht geben, einen bestimmten Vertrag abzuschließen. Mit anderen Worten: Optionen geben dem Inhaber ein Wahlrecht (und genau das ist auch die Übersetzung des englischen Wortes option).

Hobbyanleger wissen, dass man damit sehr viel Geld verlieren kann, aber die wenigsten wissen, worauf sie mit einer Option eigentlich spekulieren. Die Formel, die wir aus den beiden Kuchenstücken hergeleitet haben, sagt es uns aber: Wir spekulieren auf einen zunehmenden Unterschied zwischen F und K. Viele denken, dass wir auf einen steigenden Wert der Auszahlungsmöglichkeiten spekulieren (in dem Kuchenbeispiel wäre das z.B. ein steigendes F oder auch ein steigendes p) – das stimmt aber nicht. Denn würden wir das tatsächlich tun, dann könnten wir das billiger haben, indem wir ein Finanzinstrument kaufen, das uns nach oben wie nach unten beteiligt. Indem wir das nicht tun, zahlen wir den hohen Preis für das Wahlrecht, und dieser Preis steigt bei zunehmendem Unterschied von F und K. In der Finanztheorie würde man das Volatilität (Schwankungsintensität) nennen.

Mit anderen Worten: Eine Option ist das geeignete Instrument, wenn man auf eine zunehmende Volatilität spekuliert, also auf ein Zunehmen des möglichen Unterschieds zwischen den Spielausgängen.

Allerdings hinkt der Vergleich ein wenig, weil in dem Kuchen-Modell die Zeit nicht vorkommt, diese aber in der Options(preis)theorie eine wesentliche Rolle spielt. Das Prinzip ist jedoch durchaus das gleiche.

Werden wir philosophischer: Wählen wir freiwillig, wählen zu dürfen?

Jetzt eine Frage zweiter Ordnung: Wenn wir wählen dürfen, ob wir wählen dürfen, nehmen wir dann an? Diese Frage klingt schwieriger als sie ist, denn wir brauchen sie nur umzuformulieren in: Kann der Wert des Wahlrechts jemals negativ sein? Denn wenn das Wahlrecht für uns immer gut (oder wenigstens neutral ist), dann können wir gefahrlos immer wählen, wählen zu dürfen – im schlimmsten Fall lassen wir anschließend dieses Recht einfach verfallen.

Zum Glück haben wir oben schon die Formel hergeleitet, die uns sagt, wieviel das Wahlrecht wert ist. Wir müssen nur noch klären, ob dieser Wert W jemals negativ sein kann. Erinnern wir uns:

W = (1-p) (F-K), und es gilt

Da Wahrscheinlichkeiten niemals negativ sein können, ist (1-p) auch nie negativ; und weil wir angenommen haben, F sei nie kleiner als K, wird auch der zweite Ausdruck (F-K) niemals negativ; und deshalb kann W (der Wert des Wahlrechts) niemals negativ werden. Schon ist die Frage beantwortet. Wenn wir wählen dürfen, ob wir wählen dürfen, sagen wir immer ja.

Jetzt fragen Sie vielleicht, ob wir nicht ein bisschen zu weit gegangen sind in der Annahme, dass F immer größer oder gleich K sei. Was, wenn es auf einmal andersherum ist? Das würde unsere Überlegungen nicht stören. Denn dann würden wir bei Ausübung des Wahlrechts eben K wählen anstatt F. Die Annahme dass F größer gleich K ist, erfolgt also „ohne Beschränkung der Allgemeingültigkeit“, wie es in der Mathematik so schön heißt.

Fragen wir uns der Vollständigkeit halber, wodurch ein Wahlrecht wertlos würde. Die Antwort lautet: wenn entweder (1-p) oder (F-K) null würde oder beide. Was heißt das? Wenn (1-p) gleich null ist, dann ist p offenbar gleich eins; und das heißt, dass ohnehin nur das schöne Ereignis F (Frankfurter Kranz) eintreten kann – wozu sollten wir dann noch wählen wollen? Und wenn (F-K) gleich null wird, dann heißt das, dass beide Alternativen gleich gut oder gleich schlecht sind – eben gleich. Mit anderen Worten, in beiden Fällen haben wir faktisch nichts zu wählen, und dadurch wird das Wahlrecht wertlos.

War es das schon zum Wahlrecht?

Sind Sie enttäuscht, dass es so einfach war? Misstrauisch, dass da irgend etwas nicht stimmen kann? Warten Sie es ab, die Fortsetzung folgt. Aber ich erzähle Ihnen schon einmal eine kleine Geschichte:

Nach dem Pisa-Schock sind alle Kultusministerien aufgescheucht. Und so trudeln derzeit Vorschläge bei Universitäten und Schulen ein, diesen mehr Flexibilität, also Wahlmöglichkeiten, zu geben. Schulen sollen selbst entscheiden dürfen, wofür sie Gelder ausgeben (nicht, dass es mehr Geld gäbe, aber immerhin die Möglichkeit, diese nach eigenen Vorstellungen auszugeben); Universitäten sollen die Wahlmöglichkeit bekommen, Professoren unterschiedliche Deputate (also Lehrverpflichtungen) zu geben. Das sind alles Wahlrechte, die eigentlich nicht negativ sein dürften. Wie reagieren die Lehrer und Professorinnen? Überwiegend mögen sie diese Wahlmöglichkeiten nicht. Wieso eigentlich?

Lesen Sie hier, wieso ein Wahlrecht negativ sein kann und welche wichtigen Aspekte in dieser Analyse bisher noch fehlen.

 

---

[1]          Ja: ich meine den Nutzen im Sinne der Spieltheorie und der Ökonomie, aber dieser Begriff ist mir zu sehr mit mathematischem Hintergrund belastet.

[2]          100% ist eine Kurzschreibweise für 100/100 (hundert Hundertstel) und das ist gleich 1.

[3]          Die zugehörige Mathematik vergessen? Dann probieren Sie es folgendermaßen:
W = F – [p F + (1-p) K] = F – [p F + K – p K] = F – p F – K + p K = (1-p) F – (1-p) K = (1-p)(F-K)